☰

圓州率
🌐
☰

Feature Image

支持向量機 (Support Vector Machine, SVM)

數學, 資料科學, 機器學習, 監督式學習
以超平面 (Hyperplanes) 作為切分方法的監督式機器學習。
   最後更新:

Separating Hyperplanes

Separating Hyperplanes 的目標是在高維度空間找超平面，並最小化分類錯誤率。與回歸模型會用上所有資料點不同，超平面的建構只與不同類別資料的交界處有關。

給定 Y∈{1,−1}Y \in \{1, -1\}，考慮 linear regression

f(x)=β0+βTx \begin{align*} f (x) = \beta_0 + \beta^T x \end{align*}

其中的一個切平面

{x:f(x)=0}={x:β0+βTx=0} \begin{align*} \{ x : f (x) = 0 \} = \{ x : \beta_0 + \beta^T x = 0 \} \end{align*}

以 f(x)f (x) 的正負號決定 YY 是要預測成 11 還是 −1-1 類別。然而這並不能保證分類的準確度，原因是 linear regression 的目標是最小化 SSE，而非最小化分類錯誤率。類似的，logistic regression 也能找一個切平面，但其目標是最小化 cross entropy loss，也非是最小化分類錯誤率，並非直接以最小化錯誤率為出發點。

Perceptron Learning

Perceptron (感知器) 函數 I(x>c)I (x > c)，與 c=0c = 0 的特例

sign(x)={1if x>0−1if x≤0 \begin{align*} \text{sign} (x) = \begin{cases} 1 & \text{if} \ x > 0 \newline -1 & \text{if} \ x \leq 0 \end{cases} \end{align*}

若 y=sign(f(x))y = \text{sign}(f (x))，則表示分類正確，反之則分類錯誤。

若目標是「將高維度空間切分，並最小化預測錯誤點與切平面距離」，考慮以下 loss function

D(β0,β)=−∑i∈Myi(β0+βTxi) \begin{align*} D (\beta_0, \beta) = - \sum_{i \in M} y_i (\beta_0 + \beta^T x_i) \end{align*}

其中 MM 是分類錯誤的編號。對於 i∈Mi \in M 會有 sign(yi)=−sign(β0+βTxi)\text{sign} (y_i) = -\text{sign} (\beta_0 + \beta^T x_i)，使得 DD 函數非負。

定義資料是可分的 (separable)，即存在超平面使得平面兩側的 YY 分類結果全對。而 Perceptron Learning 有以下特徵

  1. 分割的的方式不唯一，即此分類法的結果不唯一。
  2. 若資料是線性可分的，則此方式一定能在有限步驟中找出其中一解，但有限可能是非常大的數字。
  3. 若資料是線性不可分的，則 Perceptron Learning 可能陷入無限循環使得無法收斂到任一結果。

Support Vector Machine (SVM)

若以「不同類別資料與超平面的距離」做為模型評估標準，則正確分類的資料與超平面距離越大則表示能把資料分的越開，而與超平面最近的點則稱為支持向量 (support vector)，SVM 的目標就是找到不同資料的交界處中，能使資料分隔最開的向量，即找到 support vector。

一般而言切平面能較容易在更高維度中實現，例如透過多項式將資料投射至更高維度 h(x)=(x,x2,x3)h (x) = (x, x^2, x^3)，脫離只在一維度空間找切平面，而是在三維空間找切平面

f(x)=β0+βTh(x) \begin{align*} f (x) = \beta_0 + \beta^T h (x) \end{align*}

最終再以 f~(x)=sign(f(x))\tilde f (x) = \text{sign} (f (x)) 作為預測即果，此方式找的分類邊界非線性 (non-linear boundaries)，而是稱為 generally linear boundaries。

對於資料的高維度投影 hh，常用的 kernel function 如下

  1. ddth-degree polynomial: K(x,x′)=(1+⟨x,x′⟩)dK (x, x') = (1 + \angles{x, x'})^d
  2. Radial basis: K(x,x′)=exp⁡(−γ∥x−x′∥2)K (x, x') = \exp (- \gamma \norm{x - x'}^2)
  3. Neural network: K(x,x′)=tahn(κ1⟨x,x′⟩+κ2)K (x, x') = \text{tahn} (\kappa_1 \angles{x, x'} + \kappa_2)

Tuning

SVM 能解決非線性邊界，但尋找非線性分割的運算量較為龐大，且非線性的可能太多，需進行參數調整或嘗試不同的 kernel。參考台大的 A Practical Guide to Support Vector Classification，幾個建議如下

  1. 標準化
  2. 用 Radial basis 作為 kernel
  3. 用 cross-validation 選擇參數

R 語言範例

用 e1071 包執行 SVM，並載入 packages

library(caret)      # model training
library(e1071)      # SVM
library(dplyr)      # %>%

R

以 iris 作為範例，分割成 train 與 test

data = iris
# sampling
set.seed(0)
trainIndex = createDataPartition(iris$Species, p = 0.7, list = FALSE)
train = iris[trainIndex, ]
test = iris[-trainIndex, ]

R

其中的 method 建議選用 svmRadial

# train
svm_model = train(Species ~ ., 
                  data = train, 
                  trControl = trainControl(method = "cv", number = 10), 
                  method = "svmRadial" # svmLinear, svmPoly, svmRadial
                  )

R

結果表現

# confusion matrix
predictions = predict(svm_model, test, type = "raw")
confusionMatrix(predictions, test$Species)

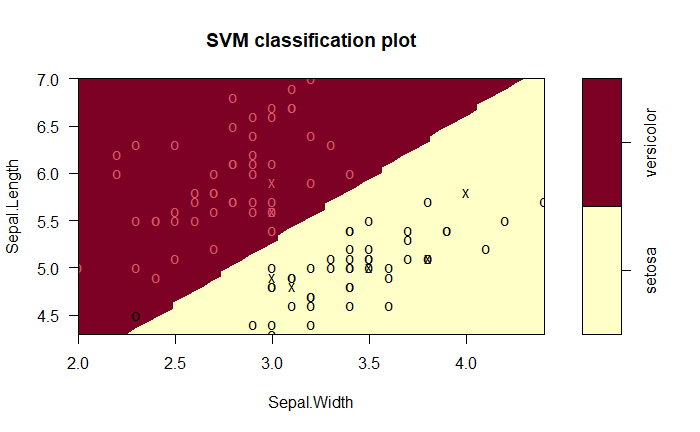
R

若資料是2維度的，可以用 plot 繪製

plot(svm_model, data)

R

參考資料

  1. The Element of Statistical Learning, Second Edition
  2. Kno's SML 2024
  3. A Practical Guide to Support Vector Classification