數獨求解器
用演算法解數獨問題。
解法簡介
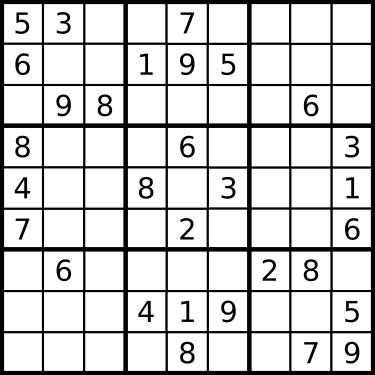
就不贅述數獨的規則了,詳見數獨介紹。以此圖為例
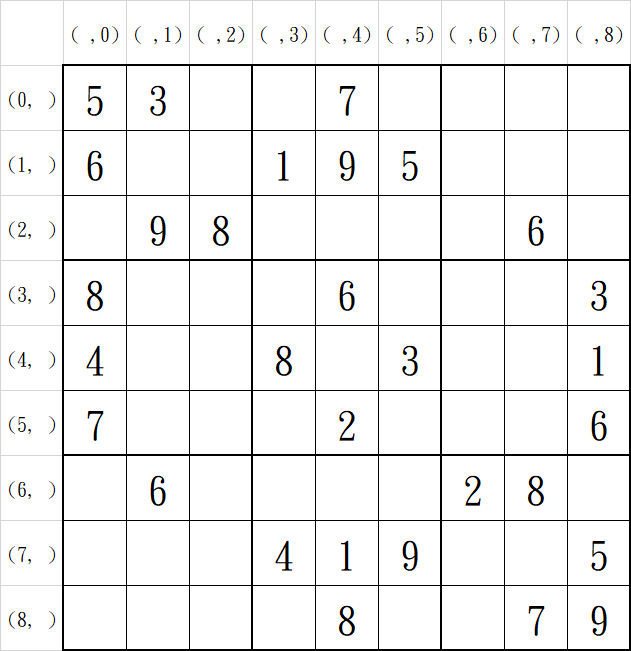
定義座標
已知每個格子能填入1到9,而填入時需要驗證3個唯一性
列唯一性
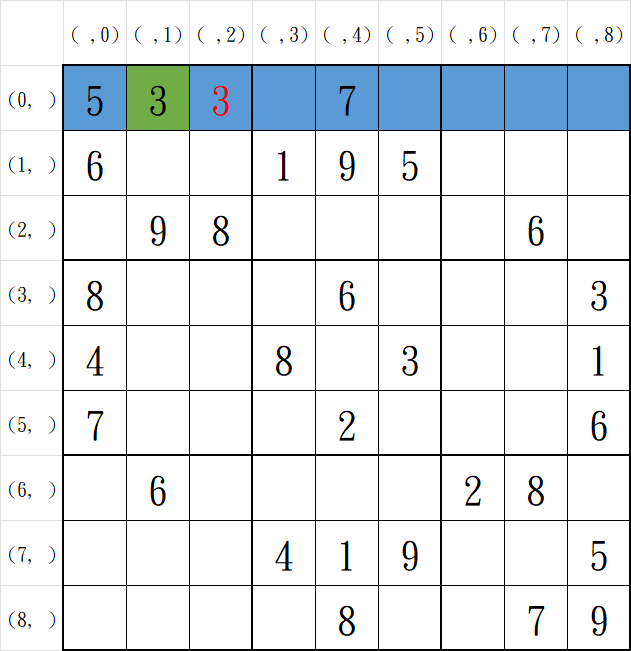
例:(0, 2)不能填入3,會和(0, 1)的3產生衝突
行唯一性
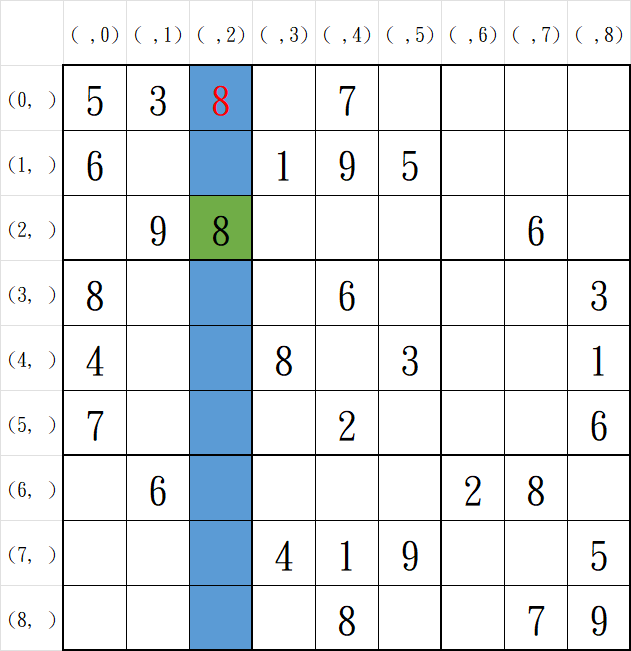
例:(0, 2)不能填入8,會和(2, 2)的8產生衝突
區唯一性
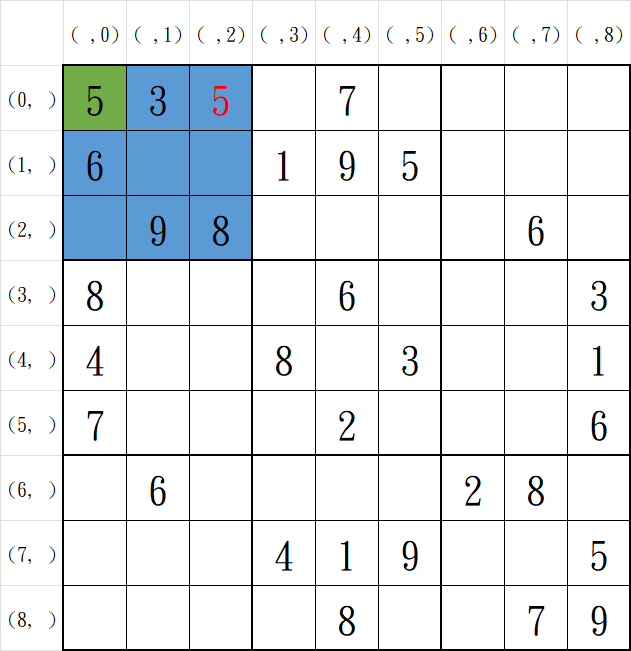
例:(0, 2)不能填入5,會和(0, 0)的5產生衝突
範例
仍用同一張圖做為範例,將未知格視為0

將由上至下,由左至右找出未知格的位置
| 座標\數值 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| (0, 2) | v | |||||||||
| (0, 3) | v | |||||||||
| (0, 5) | v | |||||||||
| … | ||||||||||
| (8, 6) | v |
首先在第一個未知格(0, 2),往後選取一個元素,也就是填入1,發現能通過唯一性驗證。
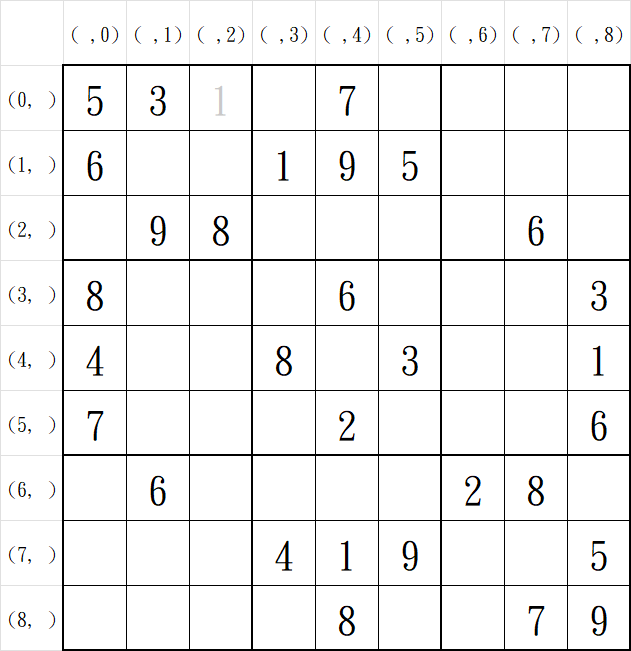
| 座標\數值 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| (0, 2) | v | |||||||||
| (0, 3) | v | |||||||||
| (0, 5) | v | |||||||||
| … |
接著在下一個未知格(0, 3),往後選取一個元素,也就是填入1,發現列唯一性不通過
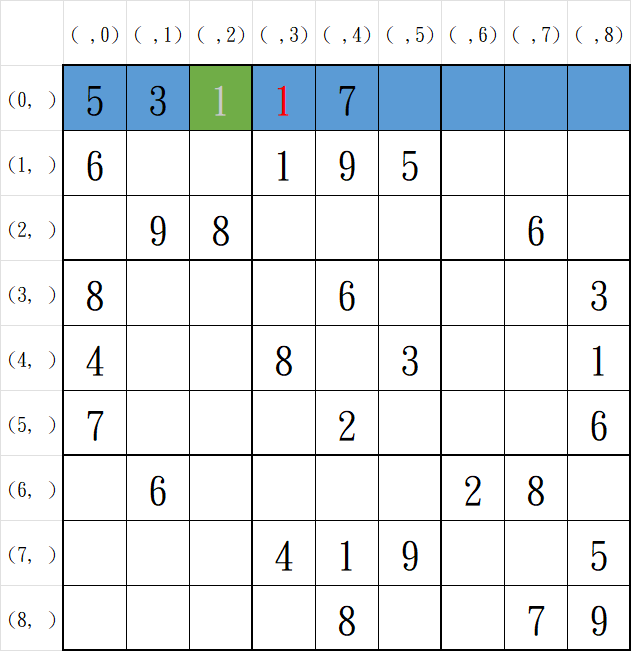
再繼續往後選取一個元素,也就是填入2,發現能通過唯一性驗證。
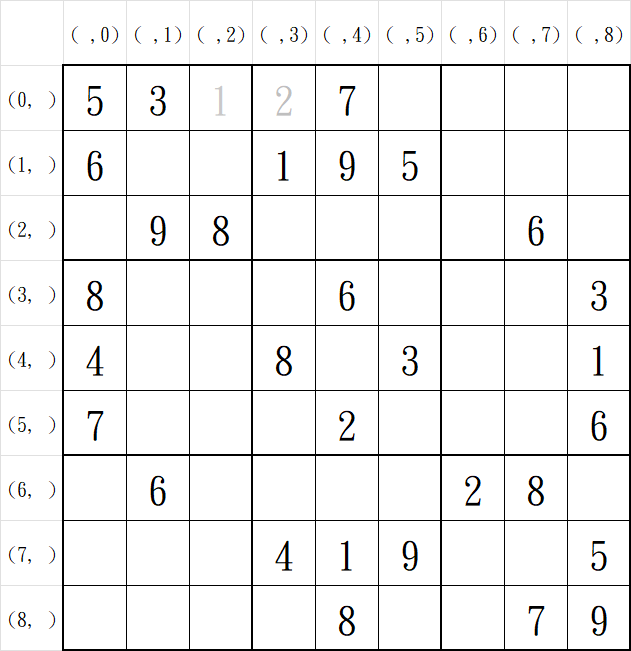
| 座標\數值 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| (0, 2) | v | |||||||||
| (0, 3) | v | |||||||||
| (0, 5) | v | |||||||||
| … |
接著在下一個未知格(0, 5)重複上述動作,會發現1, 2, 3都不通過唯一性驗證,因此填入4。
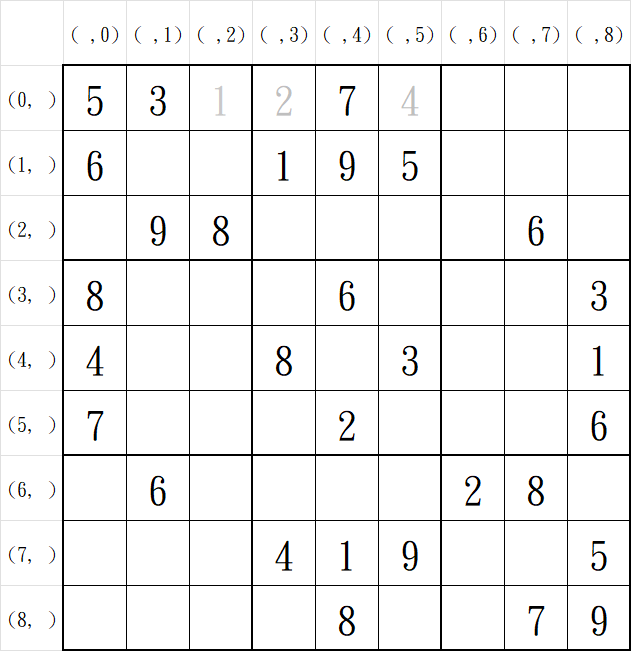
| 座標\數值 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| (0, 2) | v | |||||||||
| (0, 3) | v | |||||||||
| (0, 5) | v | |||||||||
| … |
重複上述步驟,依序對每個未知格操作
每次都填入第一個能滿足唯一性的驗證的元素
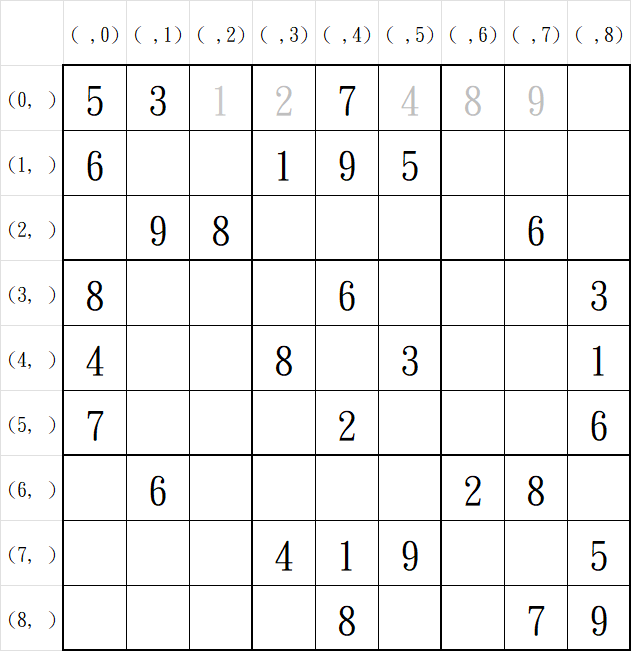
| 座標\數值 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| (0, 2) | v | |||||||||
| (0, 3) | v | |||||||||
| (0, 5) | v | |||||||||
| (0, 6) | v | |||||||||
| (0, 7) | v | |||||||||
| (0, 8) | v | |||||||||
| … |
接著在(0, 8)這格,會發現所有元素皆無法通過唯一性驗證,這表示前面的未知格一定存在錯誤。回到上一個未知格,試著填入下一個可行的元素。
但此時(0, 7)的元素是9,已經是最後一個元素,這依舊表示前面的未知格一定存在錯誤。將(0, 7)歸零後,再繼續回到上一個未知格(0, 6),試著填入下一個可行的元素,也就是填入9。
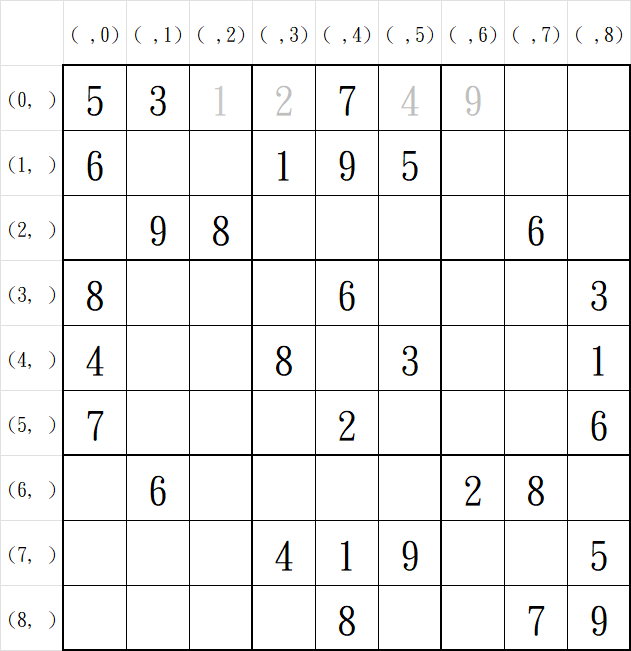
| 座標\數值 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| (0, 2) | v | |||||||||
| (0, 3) | v | |||||||||
| (0, 5) | v | |||||||||
| (0, 6) | v | |||||||||
| (0, 7) | v | |||||||||
| (0, 8) | v | |||||||||
| … |
藉由上述規則 ,我們可以遍歷所有可能的選項。簡言而之,基本概念是
一步一步對未知格填入內容,若無法填入即表示存在錯誤,把當前未知格歸零後,往後退回一步再次嘗試下一個元素。
演算法
我們可以藉由下列方式快速遍歷所有可能的選項
- 移動到下一個未知格
- 查看此格內容
- 若此格內為0~8,填入下一個元素(0的下一個元素是1,1的下一個元素是2,以此類推)
- 若此格內為9,將此格設為0,移動到上一個未知格,重新執行第2步
- 驗證三個唯一性
- 若通過,則回到第1步
- 若不通過,則回到第2步
第2步的查看內容,就是驗證是否為最後一個元素。可以將此方式擴展開,一般的數獨為9x9的大小,我們可以擴展成16x16的數獨,用相同的邏輯來處理
- 查看此格內容
- 若此格內為0~15,填入下一個元素(0的下一個元素是1,1的下一個元素是2,以此類推)
- 若此格內為16,將此格設為0,移動到上一個未知格,重新執行第2步
等價於
- 驗證是否為最後一個元素
- 若否,則填入下一個元素
- 若是,則將此格歸零,移動到上一個未知格,重新執行第2步
最後再加上完成與無解檢測。
完整的演算法為
- 移動到下一個未知格。若無下一個未知格,即表示完成
- 驗證是否為最後一個元素
- 若否,則填入下一個元素
- 若是,則將此格歸零,移動到上一個未知格,重新執行第2步。若無上一個未知格,即表示無解
- 驗證三個唯一性
- 若不通過,則回到第2步
- 若通過,則回到第1步