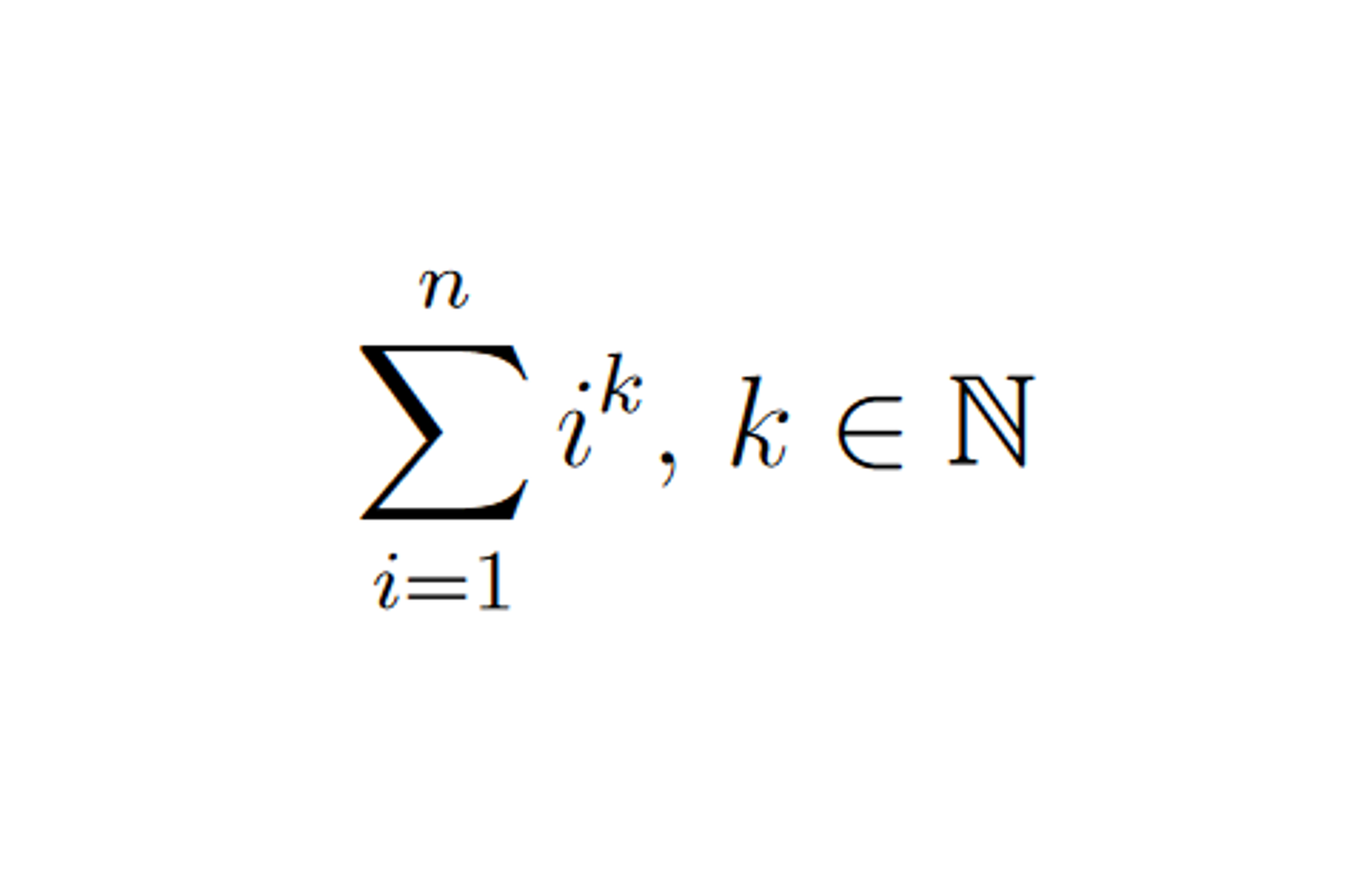k 次方求和問題 解 k 次方求和問題。
2023/07/07
最後更新:
2024/07/02 呈現部分成果
連結是計算至 ∑ i = 1 n i 100 \sum_{i = 1}^{n} i^{100} ∑ i = 1 n i 100 結果
介紹 任給一數 k ∈ N k \in \mathbb{N} k ∈ N ∑ i = 1 n i k \sum_{i = 1}^{n} i^k ∑ i = 1 n i k k = 2 k = 2 k = 2
∑ i = 1 n i 2 = 1 3 n 3 + 1 2 n 2 + 1 6 n 1
\begin{align*}
\sum_{i = 1}^{n} i^2
= \frac{1}{3} n^3 + \frac{1}{2} n^2 + \frac{1}{6} n^1
\end{align*}
i = 1 ∑ n i 2 = 3 1 n 3 + 2 1 n 2 + 6 1 n 1 關鍵步驟在於
n k = ∑ i = 1 n i k − ∑ i = 1 n ( i − 1 ) k
\begin{align*}
n^k
= \sum_{i = 1}^n i^k
- \sum_{i = 1}^n (i - 1)^k
\end{align*}
n k = i = 1 ∑ n i k − i = 1 ∑ n ( i − 1 ) k 範例 從 k = 0 k = 0 k = 0
∑ i = 1 n i 0 = ∑ i = 1 n 1 = n
\sum_{i = 1}^{n} i^0
= \sum_{i = 1}^{n} 1
= n
i = 1 ∑ n i 0 = i = 1 ∑ n 1 = n 對 k = 1 k = 1 k = 1
n 2 = ∑ i = 1 n i 2 − ∑ i = 1 n ( i − 1 ) 2 = ∑ i = 1 n [ i 2 − ( i − 1 ) 2 ] = ∑ i = 1 n ( 2 i − 1 ) = 2 ∑ i = 1 n i − ∑ i = 1 n 1
\begin{align*}
n^2
& = \sum_{i = 1}^{n} i^2 - \sum_{i = 1}^{n} (i - 1)^2 \newline
& = \sum_{i = 1}^{n} \left[ i^2 - (i - 1)^2 \right] \newline
& = \sum_{i = 1}^{n} (2i - 1) \newline
& = 2 \sum_{i = 1}^{n} i - \sum_{i = 1}^{n} 1
\end{align*}
n 2 = i = 1 ∑ n i 2 − i = 1 ∑ n ( i − 1 ) 2 = i = 1 ∑ n [ i 2 − ( i − 1 ) 2 ] = i = 1 ∑ n ( 2 i − 1 ) = 2 i = 1 ∑ n i − i = 1 ∑ n 1 將 ∑ i = 1 n i \sum_{i = 1}^{n} i ∑ i = 1 n i
∑ i = 1 n i = 1 2 ( n 2 + ∑ i = 1 n 1 ) = 1 2 n 2 + 1 2 n
\begin{align*}
\sum_{i = 1}^{n} i
& = \frac{1}{2} \left( n^2 + \sum_{i = 1}^{n} 1 \right) \\
& = \frac{1}{2} n^2 + \frac{1}{2} n
\end{align*}
i = 1 ∑ n i = 2 1 ( n 2 + i = 1 ∑ n 1 ) = 2 1 n 2 + 2 1 n 同理,當 k = 2 k = 2 k = 2
n 3 = ∑ i = 1 n i 3 − ∑ i = 1 n ( i − 1 ) 3 = ∑ i = 1 n [ i 3 − ( i − 1 ) 3 ] = ∑ i = 1 n ( 3 i 2 − 3 i + 1 ) = 3 ∑ i = 1 n i 2 − 3 ∑ i = 1 n i + ∑ i = 1 n 1
\begin{align*}
n^3
& = \sum_{i = 1}^{n} i^3
- \sum_{i = 1}^{n} (i - 1)^3 \\
& = \sum_{i = 1}^{n} \left[ i^3 - (i - 1)^3 \right] \\
& = \sum_{i = 1}^{n} (3i^2 - 3i + 1) \\
& = 3 \sum_{i = 1}^{n} i^2 - 3 \sum_{i = 1}^{n} i + \sum_{i = 1}^{n} 1
\end{align*}
n 3 = i = 1 ∑ n i 3 − i = 1 ∑ n ( i − 1 ) 3 = i = 1 ∑ n [ i 3 − ( i − 1 ) 3 ] = i = 1 ∑ n ( 3 i 2 − 3 i + 1 ) = 3 i = 1 ∑ n i 2 − 3 i = 1 ∑ n i + i = 1 ∑ n 1 將 ∑ i = 1 n i 2 \sum_{i = 1}^{n} i^2 ∑ i = 1 n i 2
∑ i = 1 n i 2 = 1 3 ( n 3 + 3 ∑ i = 1 n i − ∑ i = 1 n 1 ) = 1 3 ( n 3 + 3 [ 1 2 n 2 + 1 2 n ] − n ) = 1 3 n 3 + 1 2 n 2 + 1 6 n
\begin{align*}
\sum_{i = 1}^{n} i^2
& = \frac{1}{3} \left( n^3 + 3 \sum_{i = 1}^{n} i - \sum_{i = 1}^{n} 1 \right) \\
& = \frac{1}{3} \left( n^3 + 3 \left[ \frac{1}{2} n^2 + \frac{1}{2} n \right] - n \right) \\
& = \frac{1}{3} n^3 + \frac{1}{2} n^2 + \frac{1}{6} n
\end{align*}
i = 1 ∑ n i 2 = 3 1 ( n 3 + 3 i = 1 ∑ n i − i = 1 ∑ n 1 ) = 3 1 ( n 3 + 3 [ 2 1 n 2 + 2 1 n ] − n ) = 3 1 n 3 + 2 1 n 2 + 6 1 n 運用相同方式,對任意 k ∈ N k \in \mathbb N k ∈ N
n k + 1 = ∑ i = 1 n i k + 1 − ∑ i = 1 n ( i − 1 ) k + 1 = ∑ i = 1 n [ i k + 1 − ( i − 1 ) k + 1 ] = ∑ i = 1 n [ i k + 1 − ∑ j = 0 k + 1 ( k + 1 j ) i j ( − 1 ) k + 1 − j ] = ∑ i = 1 n [ i k + 1 − ( i k + 1 − ( k + 1 ) i k + ∑ j = 0 k − 1 ( k + 1 j ) i j ( − 1 ) k + 1 − j ) ] = ∑ i = 1 n [ ( k + 1 ) i k + ∑ j = 0 k − 1 ( k + 1 j ) i j ( − 1 ) k + 1 − j ] = ( k + 1 ) ∑ i = 1 n i k + ∑ i = 1 n ∑ j = 0 k − 1 ( k + 1 j ) i j ( − 1 ) k + 1 − j
\begin{align*}
n^{k + 1}
& = \sum_{i = 1}^{n} i^{k + 1} - \sum_{i = 1}^{n} (i - 1)^{k + 1} \\
& = \sum_{i = 1}^{n} \left[ i^{k + 1} - (i - 1)^{k + 1} \right] \\
& = \sum_{i = 1}^{n} \left[ i^{k + 1} - \sum_{j = 0}^{k + 1} \binom{k + 1}{j} i^{j} (-1)^{k + 1 - j} \right] \\
& = \sum_{i = 1}^{n} \left[ i^{k + 1} - \left( i^{k + 1} - (k + 1) i^{k} + \sum_{j = 0}^{k - 1} \binom{k + 1}{j} i^{j} (-1)^{k + 1 - j} \right) \right] \\
& = \sum_{i = 1}^{n} \left[ (k + 1) i^{k} + \sum_{j = 0}^{k - 1} \binom{k + 1}{j} i^{j} (-1)^{k + 1 - j} \right] \\
& = (k + 1) \sum_{i = 1}^{n} i^k
+ \sum_{i = 1}^{n} \sum_{j = 0}^{k - 1} \binom{k + 1}{j} i^{j} (-1)^{k + 1 - j}
\end{align*}
n k + 1 = i = 1 ∑ n i k + 1 − i = 1 ∑ n ( i − 1 ) k + 1 = i = 1 ∑ n [ i k + 1 − ( i − 1 ) k + 1 ] = i = 1 ∑ n [ i k + 1 − j = 0 ∑ k + 1 ( j k + 1 ) i j ( − 1 ) k + 1 − j ] = i = 1 ∑ n [ i k + 1 − ( i k + 1 − ( k + 1 ) i k + j = 0 ∑ k − 1 ( j k + 1 ) i j ( − 1 ) k + 1 − j ) ] = i = 1 ∑ n [ ( k + 1 ) i k + j = 0 ∑ k − 1 ( j k + 1 ) i j ( − 1 ) k + 1 − j ] = ( k + 1 ) i = 1 ∑ n i k + i = 1 ∑ n j = 0 ∑ k − 1 ( j k + 1 ) i j ( − 1 ) k + 1 − j 因此
∑ i = 1 n i k = 1 k + 1 [ n k + 1 + ∑ i = 1 n ∑ j = 0 k − 1 ( k + 1 j ) i j ( − 1 ) k + 1 − j ] = 1 k + 1 [ n k + 1 + ∑ j = 0 k − 1 [ ( k + 1 j ) ( − 1 ) k + 1 − j ∑ i = 1 n i j ] ]
\begin{align*}
\sum_{i = 1}^{n} i^k
& = \frac{1}{k + 1} \left[ n^{k + 1} + \sum_{i = 1}^{n} \sum_{j = 0}^{k - 1} \binom{k + 1}{j} i^{j} (-1)^{k + 1 - j} \right] \\
& = \frac{1}{k + 1} \left[ n^{k + 1} + \sum_{j = 0}^{k - 1} \left[ \binom{k + 1}{j} (-1)^{k + 1 - j} \sum_{i = 1}^{n} i^j \right] \right]
\end{align*}
i = 1 ∑ n i k = k + 1 1 [ n k + 1 + i = 1 ∑ n j = 0 ∑ k − 1 ( j k + 1 ) i j ( − 1 ) k + 1 − j ] = k + 1 1 [ n k + 1 + j = 0 ∑ k − 1 [ ( j k + 1 ) ( − 1 ) k + 1 − j i = 1 ∑ n i j ] ] 令 ∑ i = 1 n i k = S k \sum_{i = 1}^{n} i^k = S_k ∑ i = 1 n i k = S k
S k = 1 k + 1 [ n k + 1 + ∑ j = 1 k ( k + 1 j ) ( − 1 ) k − j S j ]
\begin{align*}
S_k
= \frac{1}{k + 1} \left[ n^{k + 1} + \sum_{j = 1}^{k} \binom{k + 1}{j} (-1)^{k - j} S_j \right]
\end{align*}
S k = k + 1 1 [ n k + 1 + j = 1 ∑ k ( j k + 1 ) ( − 1 ) k − j S j ] 另解 找到其他人的解法,過程真的很精妙!分享給大家
Python 實作 from fractions import Fraction
from math import comb
import numpy as np
k = int(input())
p = k + 1
A = np. zeros((p, p)) + Fraction()
for i in range(p):
for j in range(p):
if i >= j:
A[i][j] = Fraction(comb(i + 1 , j)) if (i + j) % 2 == 0 else Fraction(- comb(i + 1 , j))
else :
A[i][j] = Fraction(0 )
B = np. zeros(p) + Fraction()
B[0 ] = 1 / A[k][k]
A[k] = A[k] / A[k][k]
for i in range(1 , p):
B[i] = - A[k][k - i] / A[k - i][k - i]
A[k] = A[k] - (A[k][k - i] / A[k - i][k - i]) * A[k - i]
print(f " \\ frac {{ 1 }}{{ { p} }} n^ {{ { p} }} " , end = ' ' )
for i in range(1 , p):
if B[i]. numerator != 0 :
print("+" if B[i]. numerator > 0 else "-" , end = ' ' )
if abs(B[i]. numerator) == 1 and B[i]. denominator == 1 :
print(f "n^ {{ { p - i} }} " , end = ' ' )
elif B[i]. denominator == 1 :
print(f " { abs(B[i]. numerator)} n^ {{ { p - i} }} " , end = ' ' )
else :
print(f " \\ frac {{ { abs(B[i]. numerator)} }}{{ { B[i]. denominator} }} n^ {{ { p - i} }} " , end = ' ' )
python Copy