多階段連續製程預測 一個多階段連續製程的工廠產線資料集,本實驗透過原料數據與機台參數預測產品輸出規格。
2025/05/17
最後更新:
2025/05/29 引言 封面來自 Library of Congress. (1937, March 16). Exterior – Ford Assembly Plant East Side, showing Oil Well #6 in the foreground, northeast of the assembly plant 是福特汽車公司的工廠組裝工廠。
資料來自於 Multi-stage continuous-flow manufacturing process ,是一個真實的產線資料,由於資料的匿名性,我們無從得知這是什麼樣的產線,也無從得知當中變數的實際意義。但根據其介紹得知,首先由三台機器平行製造零件,接著經過兩階段的組合零件。目標為預測組合的成品結果,因此我們推測實際目的可能是組合成本較高,若預期成品不佳,則可以提早捨棄此樣本,能省下部分成本。
機台示意圖
生產機 1 ┐
生產機 2 ┼— 組合機 1 — 組合機 2
生產機 3 ┘
Copy
資料介紹 原始資料是一個 14,088 x 116 的表格,其中約有 14,000 個樣本與 116 個特徵,特徵包含:
時間戳 濕度 溫度 生產機 1 至 3 號的 36 個狀態,包含馬達轉速、材料狀態等 組合機 1 的 3 個狀態 組合機 1 的預期測量數值 15 個 組合機 1 的實際測量數值 15 個 組合機 2 的 14 個狀態 組合機 2 的預期測量數值 15 個 組合機 2 的實際測量數值 15 個 其中「預期測量數值」是工廠期待產品的規格,「實際測量數值」是真實生產的產品規格。根據任務描述,首要目標是預測「組合機 1 的實際測量數值 15 個」,為簡化問題先將目標設定為預測「組合機 1 的實際測量數值 1 個」。
經調整後的資料為 14,032 x 42,利用以下資訊:
濕度 溫度 生產機 1 至 3 號的 36 個狀態,包含馬達轉速、材料狀態等 組合機 1 的 3 個狀態 預測「組合機 1 的實際測量數值 1 個 Stage1.Output.Measurement0.U.Actual」。數據展示如下表,部分欄位因命名過長因此重新命名。
Humidity Temperature Machine1.RawMaterialFeederParameter Stage1.Output.Measurement0.U.Actual 17.24 23.53 1241.26 12.72 17.24 23.53 1246.09 12.34 17.24 23.53 1246.29 12.34
探索性資料分析 EDA 為簡化描述,稱預測目標 Stage1.Output.Measurement0.U.Actual 為 y y y x 1 x_1 x 1 x 41 x_{41} x 41
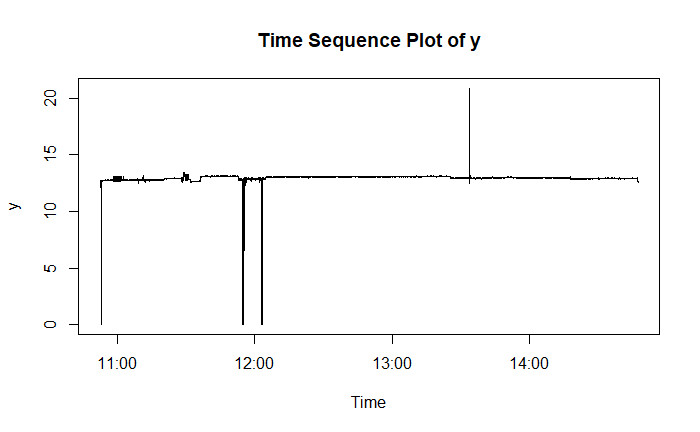
預測目標 首先值得注意的是 y y y
y y y
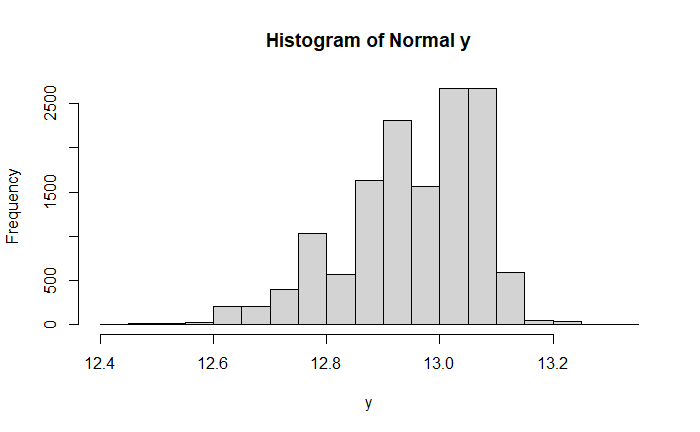
大部分的 y y y 12.9 ± 0.5 12.9 \pm 0.5 12.9 ± 0.5
正常 y y y ∈ [ 12.4 , 13.4 ] \in [12.4, 13.4] ∈ [ 12.4 , 13.4 ]
y y y 數量 比例 ≥ 13.4 \geq 13.4 ≥ 13.4 25 0.0018 12.4 ∼ 13.4 12.4 \sim 13.4 12.4 ∼ 13.4 13,975 0.9920 ≤ 12.4 \leq 12.4 ≤ 12.4 88 0.0062
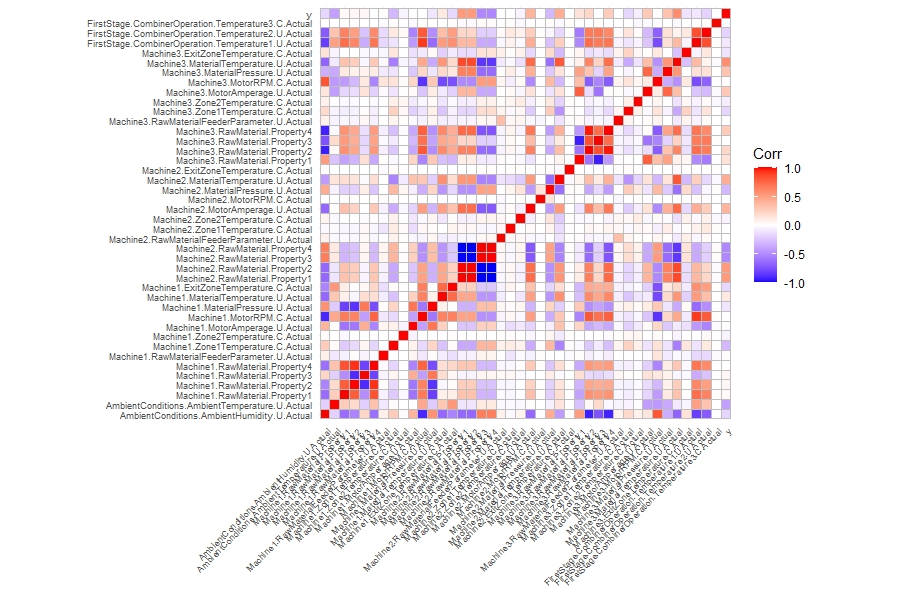
相關性 異常相關性 每筆「實際測量數值」都有其對應的「預期測量數值」,其中約有 < 1 % < 1\% < 1% 99 % 99\% 99% y y y
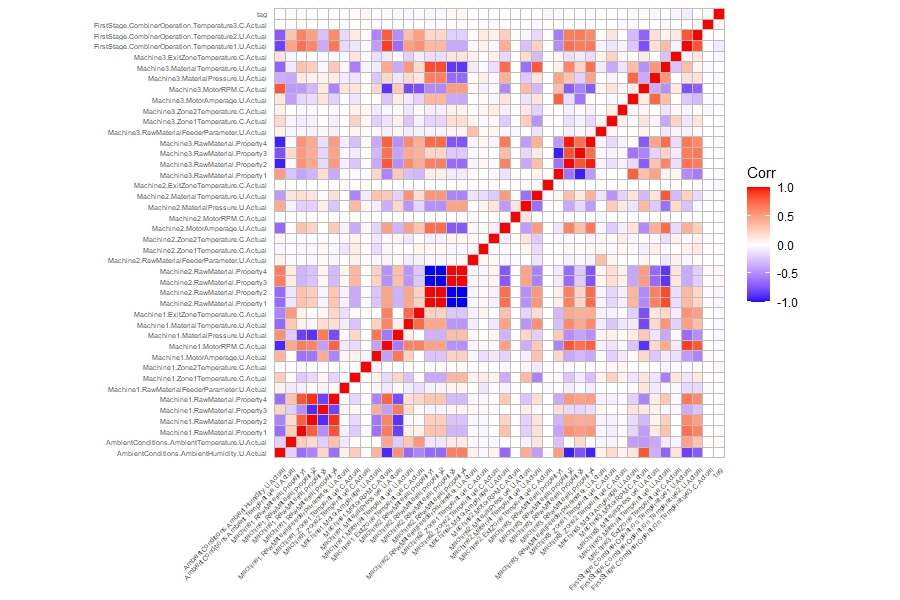
另一方面,考慮過大異常發生時的情況,令 tag \text{tag} tag tag \text{tag} tag
tag = { 1 if y > 13.4 0 if y ∈ [ 12.4 , 13.4 ] \begin{align*}
\text{tag}
= \begin{cases}
1 & \text{if } y > 13.4 \\
0 & \text{if } y \in [12.4, 13.4] \\
\end{cases}
\end{align*} tag = { 1 0 if y > 13.4 if y ∈ [ 12.4 , 13.4 ]
tag (最右側) 與變數相關係數,tag 與其他變數的相關係數接近 0。
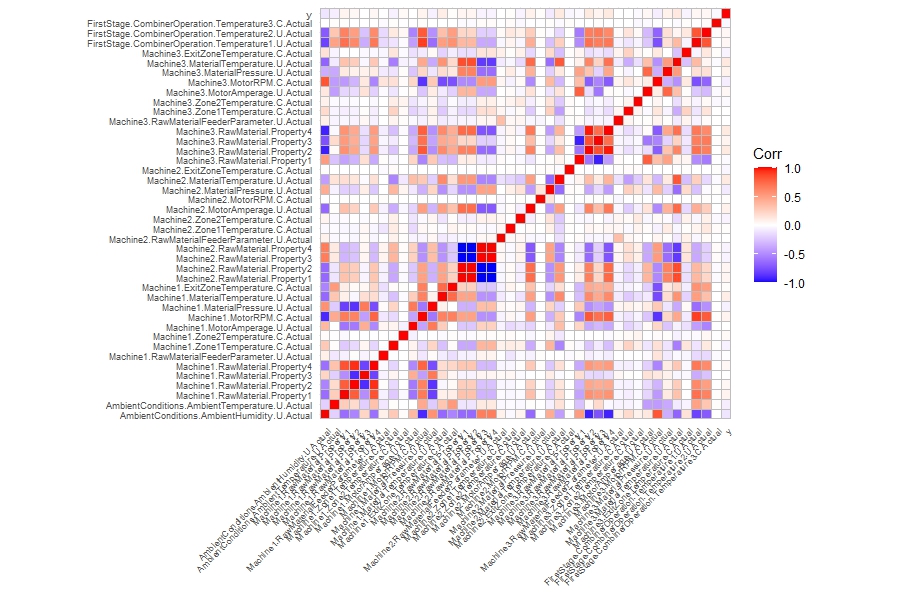
變數相關性 觀察各變數與 y y y y y y y y y y y y 99 % 99\% 99% < 1 % < 1\% < 1%
全資料相關係數,y y y
具有正常 y y y y y y
探索性小結 y y y < 1 % < 1\% < 1% 過小異常值與「預期測量數值」的設定有關。 過大異常值在相關係數與初步的建模中都難以分辨。 全體資料中, y y y 具有正常 y y y y y y 小結,暫且移除異常 y y y
建立模型 以 5-fold cv 分割資料,線性回歸做為基準模型,與最佳模型 XGBoosts,平均表現如下表
Model RMSE Rsquared Linear 0.076 0.589 XGBoost 0.044 0.863
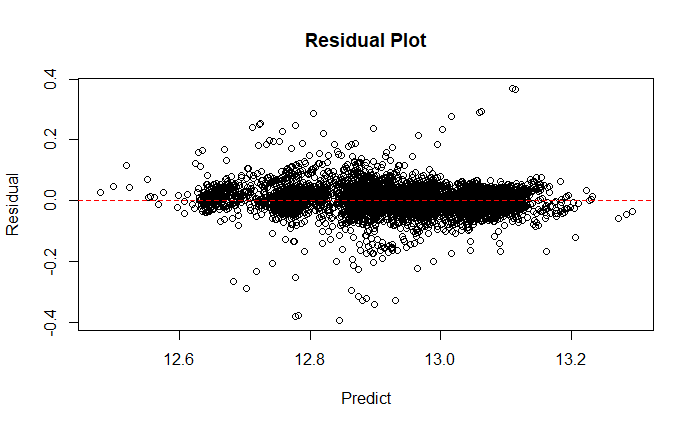
XGBoosts 殘差圖
模型解釋性 SHAP SHapley Additive exPlanations (SHAP) 是一種解釋模型的方法,啟發自博弈論 (對局論) 的關鍵人物 Lloyd Stowell Shapley 的 Shapley Value。原始的問題描述的是合作賽局理論,是將合作的總收益公平的分配給所有人的方法。
Shapley Value 有 3 個用戶合作產生收益,例如 1 號與 2 號玩家合作收益 (value) 寫成 v ( x 1 , x 2 ) = 50 v (x_1, x_2) = 50 v ( x 1 , x 2 ) = 50
Player Value x 1 x_1 x 1 10 x 2 x_2 x 2 30 x 3 x_3 x 3 5 x 1 , x 2 x_1, x_2 x 1 , x 2 50 x 1 , x 3 x_1, x_3 x 1 , x 3 35 x 2 , x 3 x_2, x_3 x 2 , x 3 40 x 1 , x 2 , x 3 x_1, x_2, x_3 x 1 , x 2 , x 3 100
則 Shaply value 計算方式為「考慮新玩家加入後所增加收益的平均」,例如原本只有 x 2 x_2 x 2 v ( x 2 ) v (x_2) v ( x 2 ) x 1 x_1 x 1 v ( x 2 , x 1 ) v (x_2, x_1) v ( x 2 , x 1 ) x 1 x_1 x 1 v ( x 2 , x 1 ) − v ( x 2 ) v (x_2, x_1) - v (x_2) v ( x 2 , x 1 ) − v ( x 2 )
Order x 1 x_1 x 1 Value x 1 , x 2 , x 3 {\color{red} x_1}, x_2, x_3 x 1 , x 2 , x 3 v ( x 1 ) v (x_1) v ( x 1 ) 10 x 1 , x 3 , x 2 {\color{red} x_1}, x_3, x_2 x 1 , x 3 , x 2 v ( x 1 ) v (x_1) v ( x 1 ) 10 x 2 , x 1 , x 3 x_2, {\color{red} x_1}, x_3 x 2 , x 1 , x 3 v ( x 2 , x 1 ) − v ( x 2 ) v (x_2, x_1) - v (x_2) v ( x 2 , x 1 ) − v ( x 2 ) 20 x 2 , x 3 , x 1 x_2, x_3, {\color{red} x_1} x 2 , x 3 , x 1 v ( x 2 , x 3 , x 1 ) − v ( x 2 , x 3 ) v (x_2, x_3, x_1) - v (x_2, x_3) v ( x 2 , x 3 , x 1 ) − v ( x 2 , x 3 ) 65 x 3 , x 1 , x 2 x_3, {\color{red} x_1}, x_2 x 3 , x 1 , x 2 v ( x 3 , x 1 ) − v ( x 3 ) v (x_3, x_1) - v (x_3) v ( x 3 , x 1 ) − v ( x 3 ) 35 x 3 , x 2 , x 1 x_3, x_2, {\color{red} x_1} x 3 , x 2 , x 1 v ( x 3 , x 2 , x 1 ) − v ( x 3 , x 2 ) v (x_3, x_2, x_1) - v (x_3, x_2) v ( x 3 , x 2 , x 1 ) − v ( x 3 , x 2 ) 65
而 x 1 x_1 x 1
ϕ 1 = 10 + 10 + 20 + 65 + 35 + 65 6 ≈ 34.17 \begin{align*}
\phi_1
= \frac{10 + 10 + 20 + 65 + 35 + 65}{6}
\approx 34.17
\end{align*} ϕ 1 = 6 10 + 10 + 20 + 65 + 35 + 65 ≈ 34.17 令 ϕ j \phi_j ϕ j j j j p p p
ϕ j = ∑ S ⊆ { x 1 , x 2 , ⋯ , x p } \ { x j } ∣ S ∣ ! ( p − ∣ S ∣ − 1 ) ! p ! ( v ( S ∪ { x j } ) − v ( S ) ) \begin{align*}
\phi_j
= \sum_{S \subseteq \{ \contia{x}{p} \} \backslash \{ x_j \} } \frac{|S| ! (p - |S| - 1) !}{p!} (v (S \cup \{ x_j \}) - v (S))
\end{align*} ϕ j = S ⊆ { x 1 , x 2 , ⋯ , x p } \ { x j } ∑ p ! ∣ S ∣ ! ( p − ∣ S ∣ − 1 )! ( v ( S ∪ { x j }) − v ( S )) 可以理解為選擇玩家 x j x_j x j j j j S S S S S S ∣ S ∣ ! |S|! ∣ S ∣ ! j j j ( p − ∣ S ∣ − 1 ) ! (p - |S| - 1)! ( p − ∣ S ∣ − 1 )!
S S S Order x 1 x_1 x 1 Value { } \{\} { } x 1 , x 2 , x 3 {\color{red} x_1}, x_2, x_3 x 1 , x 2 , x 3 v ( x 1 ) v (x_1) v ( x 1 ) 10 x 1 , x 3 , x 2 {\color{red} x_1}, x_3, x_2 x 1 , x 3 , x 2 { x 2 } \{x_2\} { x 2 } x 2 , x 1 , x 3 x_2, {\color{red} x_1}, x_3 x 2 , x 1 , x 3 v ( x 2 , x 1 ) − v ( x 2 ) v (x_2, x_1) - v (x_2) v ( x 2 , x 1 ) − v ( x 2 ) 20 { x 3 } \{x_3\} { x 3 } x 3 , x 1 , x 2 x_3, {\color{red} x_1}, x_2 x 3 , x 1 , x 2 v ( x 3 , x 1 ) − v ( x 3 ) v (x_3, x_1) - v (x_3) v ( x 3 , x 1 ) − v ( x 3 ) 35 { x 2 , x 3 } \{x_2, x_3\} { x 2 , x 3 } x 2 , x 3 , x 1 x_2, x_3, {\color{red} x_1} x 2 , x 3 , x 1 v ( x 2 , x 3 , x 1 ) − v ( x 2 , x 3 ) v (x_2, x_3, x_1) - v (x_2, x_3) v ( x 2 , x 3 , x 1 ) − v ( x 2 , x 3 ) 65 x 3 , x 2 , x 1 x_3, x_2, {\color{red} x_1} x 3 , x 2 , x 1
則計算後可得,ϕ 1 = 34.17 \phi_1 = 34.17 ϕ 1 = 34.17 ϕ 2 = 41.66 \phi_2 = 41.66 ϕ 2 = 41.66 ϕ 3 = 24.17 \phi_3 = 24.17 ϕ 3 = 24.17
而 Shaply 的方法之所以合理,因其滿足:
效率性:所有人的貢獻和等於總價值。
∑ j = 1 p ϕ j = v ( x 1 , x 2 , ⋯ , x p ) \begin{align*}
\sum_{j = 1}^{p} \phi_j = v (\contia{x}{p})
\end{align*} j = 1 ∑ p ϕ j = v ( x 1 , x 2 , ⋯ , x p ) 對稱性:若兩個人在所有情況下對合作的影響都相同,則貢獻應相同。對任意 S ⊆ { x 1 , x 2 , ⋯ , x p } \ { x i , x j } S \subseteq \{ \contia{x}{p} \} \backslash \{ x_i, x_j \} S ⊆ { x 1 , x 2 , ⋯ , x p } \ { x i , x j }
v ( S ∪ { x i } ) = v ( S ∪ { x j } ) ⇒ ϕ i = ϕ j \begin{align*}
v (S \cup \{ x_i \}) = v (S \cup \{ x_j \})
\Rightarrow \phi_i = \phi_j
\end{align*} v ( S ∪ { x i }) = v ( S ∪ { x j }) ⇒ ϕ i = ϕ j 零貢獻為零:若某人的加入完全不影響合作價值,則其貢獻為 0。對任意 S ⊆ { x 1 , x 2 , ⋯ , x p } \ { x j } S \subseteq \{ \contia{x}{p} \} \backslash \{ x_j \} S ⊆ { x 1 , x 2 , ⋯ , x p } \ { x j }
v ( S ∪ { x j } ) = v ( S ) ⇒ ϕ j = 0 \begin{align*}
v (S \cup \{ x_j \}) = v (S)
\Rightarrow \phi_j = 0
\end{align*} v ( S ∪ { x j }) = v ( S ) ⇒ ϕ j = 0 SHapley Additive exPlanations (SHAP) 帶著 Shaply value 的觀念至機器學習裡面,考慮特徵 x 1 , x 2 , ⋯ , x p \contia{x}{p} x 1 , x 2 , ⋯ , x p y ^ \hat y y ^
模型預測值是如何由各個特徵貢獻而來的?
首先,ϕ 0 \phi_0 ϕ 0 x j x_j x j ϕ j \phi_j ϕ j
y ^ ( x ) = ϕ 0 + ∑ j = 1 p ϕ ( x ) j \begin{align*}
\hat y (x)
= \phi_0 + \sum_{j = 1}^{p} \phi (x)_j
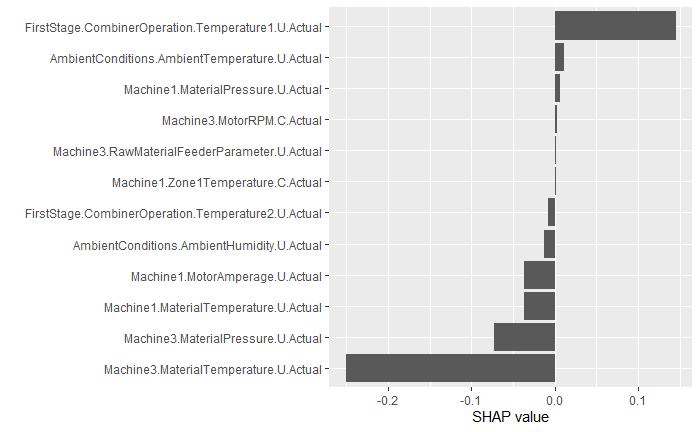
\end{align*} y ^ ( x ) = ϕ 0 + j = 1 ∑ p ϕ ( x ) j Force Plot 考慮單一預測是如何從各特徵的貢獻,知道預測高於或低於平均的理由,例如第一筆預測值低於平均 0.27,主要理由是
FirstStage.CombinerOperation.Temperature1.U.Actual 導致預測 + 0.15Machine3.MaterialTemperature.U.Actual 導致預測 - 0.25
XGBoosts SHAP Force Plot
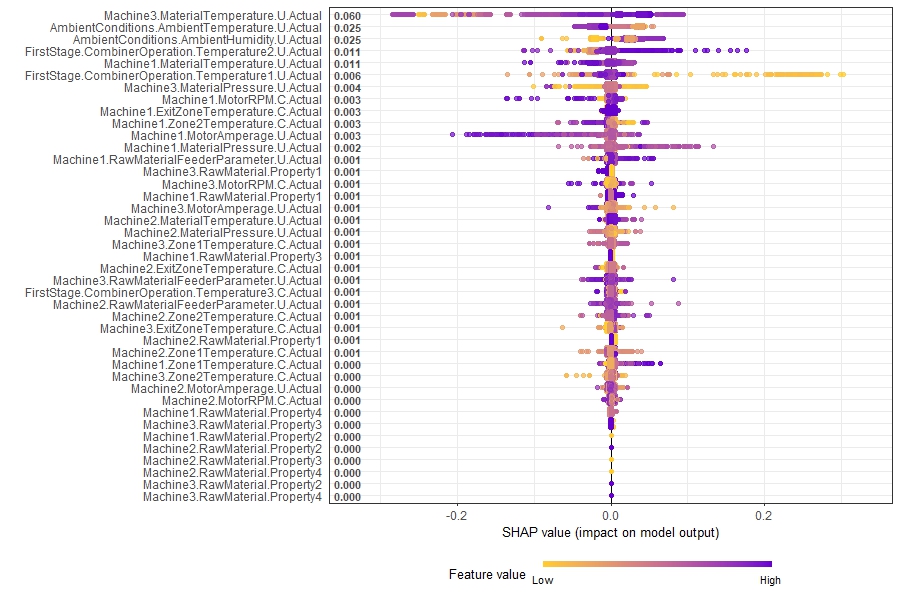
Summary Plot 若考慮全體樣本,每個點表示一個樣本,顏色表示數值大小。觀察特徵在不同大小所對應的 SHAP value,例如第一個特徵 Machine3.MaterialTemperature.U.Actual,在顏色偏黃時,SHAP < 0;也就是該數值較小時,模型傾向輸出降低 y ^ \hat y y ^
XGBoosts SHAP Summary Plot
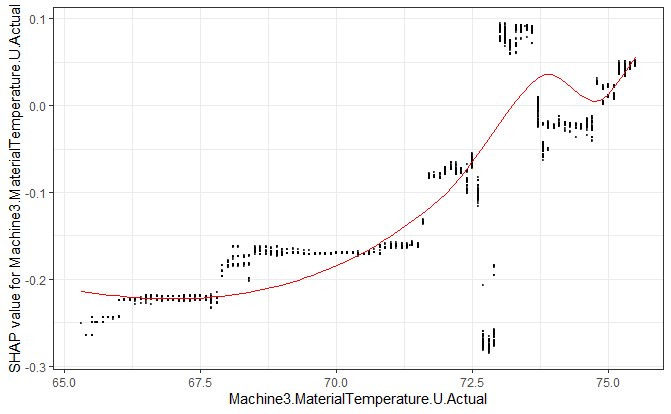
Dependence Plot 考慮單變在不同數值時對模型貢獻的差異,例如在 x x x y ^ \hat y y ^ x x x ≈ 0 \approx 0 ≈ 0
XGBoosts SHAP Dependence Plot
SHAP 考慮不同的特徵對模型的影響,但 Shaply value 的計算涉及大量排列組合,且預測時沒辦法做到"不放"某個特徵,因此更多是由區間採樣或某樣本與平均距離的差異下手,例如 Shapley Sampling 或 Kernel SHAP,甚至還有針對樹模型,如 XGBoost 的 SHAP 優化算法,方法多樣這邊就不贅述。
最後 SHAP 除了計算成本高外,使用上須注意的點主要是
不能做為因果推論,SHAP 僅解釋模型決策的「邊際貢獻 (去除一個特徵的貢獻)」,這在資料具有強共線性時更容易影響邊際貢獻。建議同時考慮相關性矩陣。 別過度解釋單一樣本,SHAP 僅考慮當下的輸入,對於局部解釋並不穩定。建議考慮一群樣本的 SHAP 值分布。 注意基準值偏誤,ϕ 0 \phi_0 ϕ 0 討論 給工廠的建議,可以怎麼調整 y y y C 則表示可控變數 (controllable),U 則為不可控制變數 (uncontrollable),因此準確的問題為
在可控變數中,如何調整 y y y
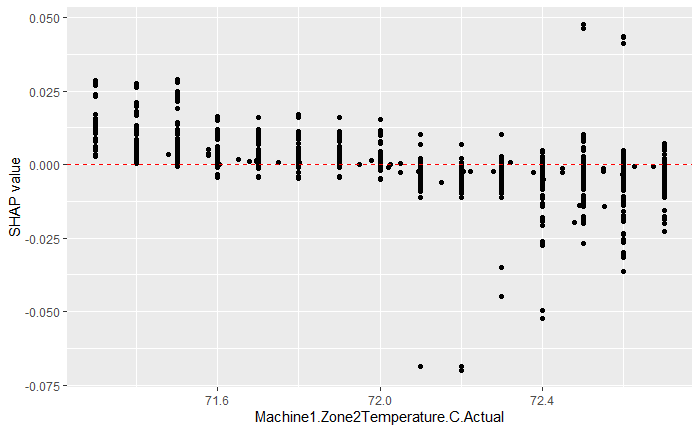
大多變數都帶有複雜的相關性,然而 Machine1.Zone2Temperature.C.Actual 與其他變數幾乎無關的同時,對 y ^ \hat y y ^ y ^ \hat y y ^ y y y y y y
SHAP Machine1.Zone2Temperature.C.Actual Dependence Plot
Machine1.Zone2Temperature.C.Actual vs y Scatter Plot
總結 存在極度異常值。部分 x x x y y y XGBoost 提供了一個較為穩定的預測模型,預測誤差落控制在 3% 以內,約 86% 的測試 R 2 R^2 R 2 SHAP 能在複雜模型裡提供解釋性。能得知單筆預測的理由,同時也能觀察群體在不同特徵時的表現。 x x x y y y Machine1.Zone2Temperature.C.Actual 就是與 y y y 參考資料 Lundberg, S. M., & Lee, S. I. (2017). A unified approach to interpreting model predictions. Advances in neural information processing systems, 30. Si, Yong, et al. (2025). Machine Learning-Based Prediction of Mortality in Geriatric Traumatic Brain Injury Patients.