機器學習介紹 (Machine Learning)
引言
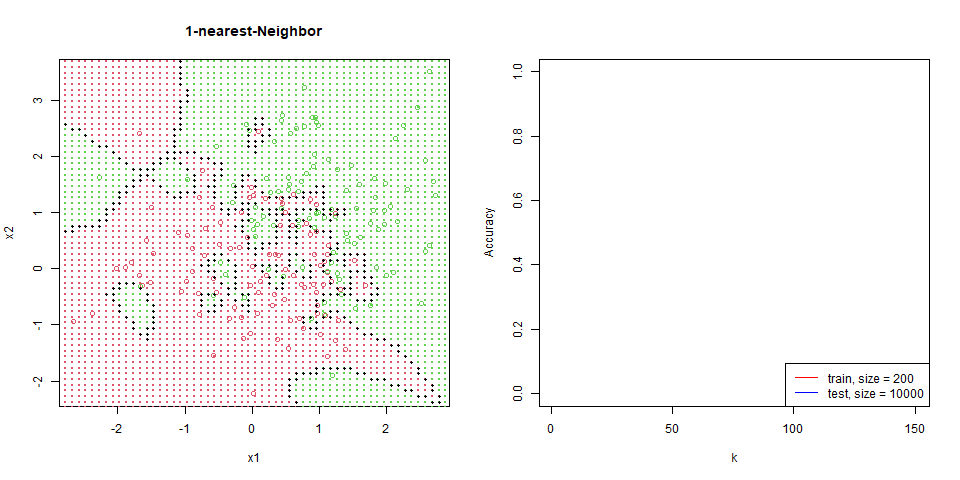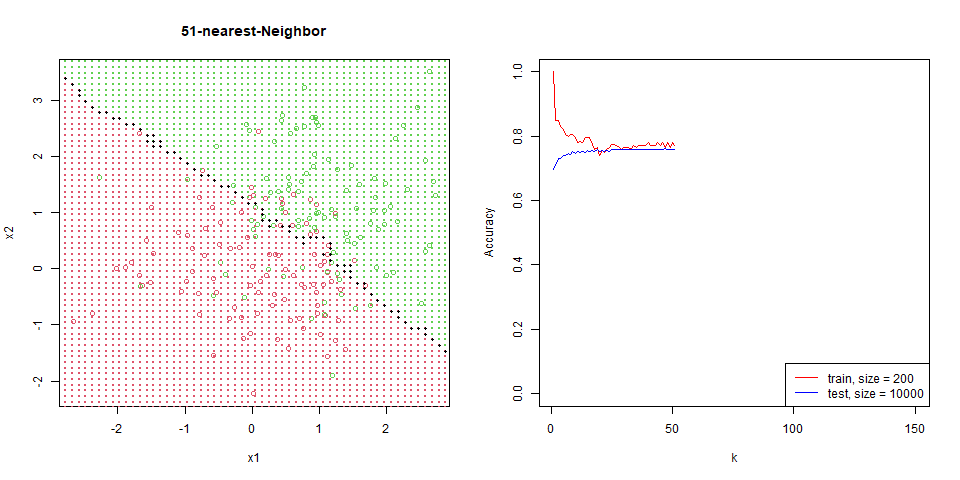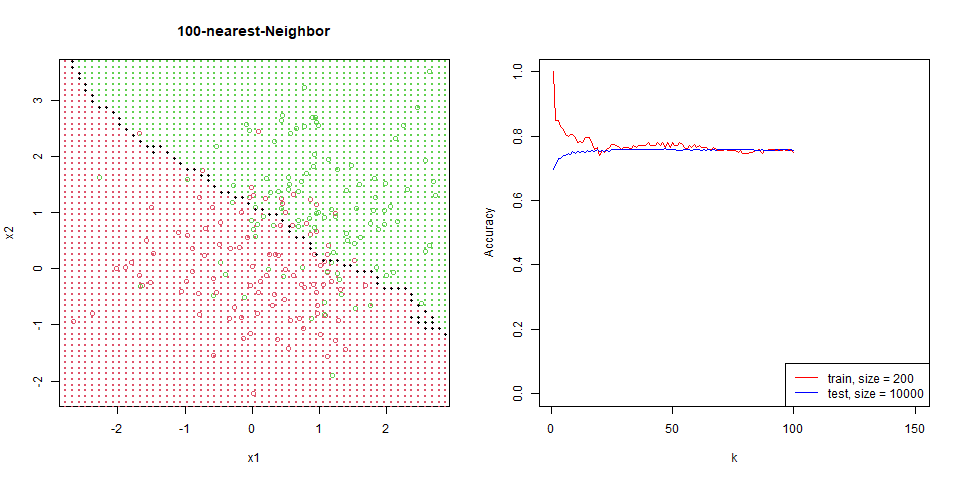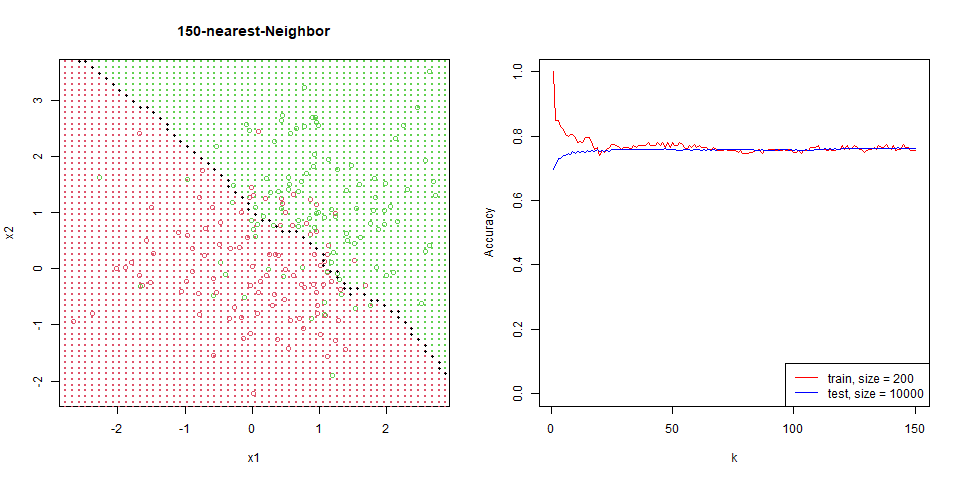
封面是本次 k nearest-neighbor 的模擬實驗結果。
所謂「機器學習」是
- 機器:即函數或演算法。
- 學習:以資料 (data-based) 作為基礎而非規則 (rule-based)。
機器學習作為資料科學的一個重要工具,其步驟可被拆解為 OCEMIC (最後的 C 與 I 合併)。
- 獲取 (Obtain)
- 清理 (Clean)
- 探索 (Explore)
- 建模 (Model)
- 解釋 (Interpret)
監督式學習 (Supervised Learning)
給定資料 ,目標是找出 與 的關聯,因此選定 在一個函數空間,並在最小化損失函數 或風險 的條件下找到最合適的 。可應用於預測。
例如手寫數字辨識,給定 是像素資料,,利用 if else 的規則來執行顯然不切實際,此時轉用基於資料 的方式,找出可行的 。
非監督式學習 (Unsupervised Learning)
給定資料 ,其中 ,目標是找出 之間的關聯,例如線性關係或是聚類。應用於推薦系統。
半監督式學習 (Semi-supervised Learning)
相較於監督式學習,半監督式學習的資料僅有部分的給定 ,例如上述的手寫數字辨識,可能基於成本使得僅有部分的資料有標記 ,因此更需要靠非監督式的方式找出 之間的關聯性,並用部分標記 的資料建立監督式學習模型。
建模類型
監督式學習目標在建構一個合適的 ,一般分為兩種類別,分別對應 對資料的敏感度。首先將資料分成兩部分,一部分用於訓練 (train) 模型,另一部分用於測試 (test) 模型的準確度。
全局 (Global)
以回歸 (regression) 作為代表,例如線性回歸對於新資料的預測,是 的線性組合,寫作
在這系列能找到更多深入的討論。回歸模型往往會帶有較強的資料假設,例如常態假設 (normal assumption)
其中 ,對整體趨勢能較好的描述,但容易被偏離值 (outlier) 影響。
局部 (Local)
以近鄰演算法 (nearest-neighbor, knn) 作為代表,對於新資料的預測,會根據其 最近的 個點所對應的 數值的平均 (或眾數),稱為 -近鄰演算法 (-nearest neighbor),定義為
其中的 是距離 最近的 個 。或者是找尋給定半徑的資料點平均 (或眾數)
其中的 ,即以 為中心,半徑為 的圓。最後,由於 ,會透過一個轉換函數轉換輸出數值
而局部模型一般帶有較弱的資料假設,例如「相近的 ,帶有相近的 」,因此即使資料在局部有較多的變化,nearest-neighbor 也能較為合適的貼近;相對的,卻很難描述出全局的資料變動趨勢。
全局 vs 局部
| 全局 | 局部 | |
|---|---|---|
| 強項 | 整體趨勢 | 局部特徵 |
| 弱點 | 受偏離值 (outlier) 影響 | 過度擬合 (overfitting) |
| 特徵 | 高 bias / 精度低 ( 與 差距大) | 高 variance / 不穩定 (train 和 test 精確度差距大) |
| 解釋性 | 高 | 低 |
接下來會給出兩個範例,每個資料 其中 。train 有 200 點,test 有 10000 點。
- 範例一:資料來自 2 個獨立且不同中心的二維常態分佈,每組資料 100 點,第 1 組資料的 標記為 0,第 2 組資料的 標記為 1。
- 範例二:資料來自 20 個獨立且不同中心的二維常態分佈,每組資料 10 點,前 5 組資料的 標記為 0,後 5 組資料的 標記為 1。
範例一
給定
且
紅點標記為 ,綠點標記為 。
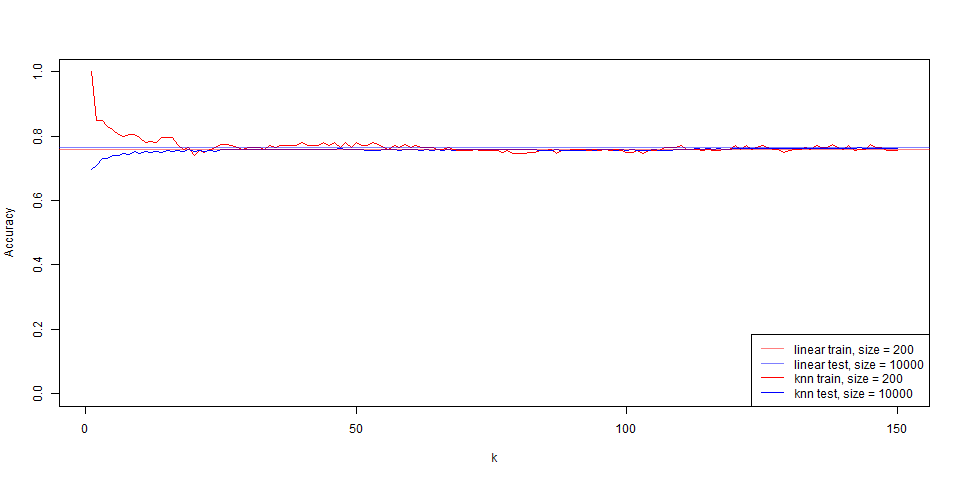
繪製出 linear regression 的區域,其 train 與 test 準確度均約為 76%。

對這筆資料進行 nearest-neighbor。
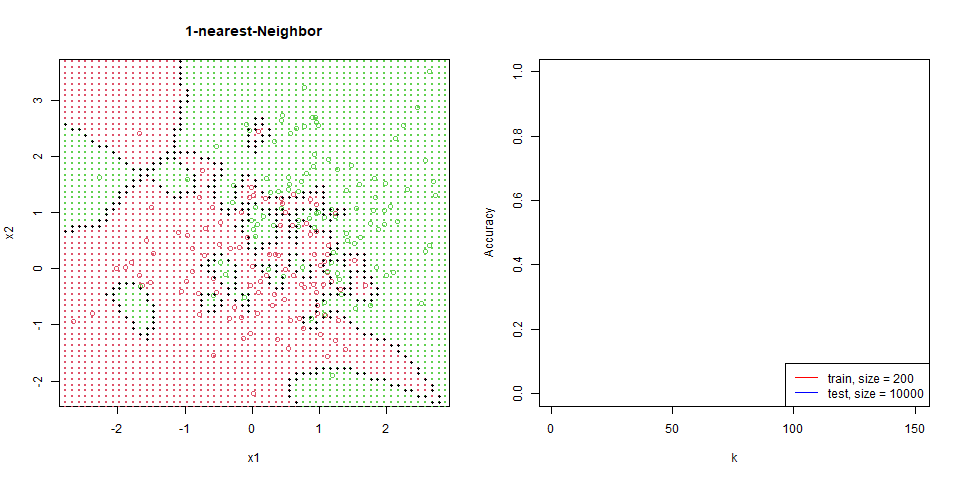
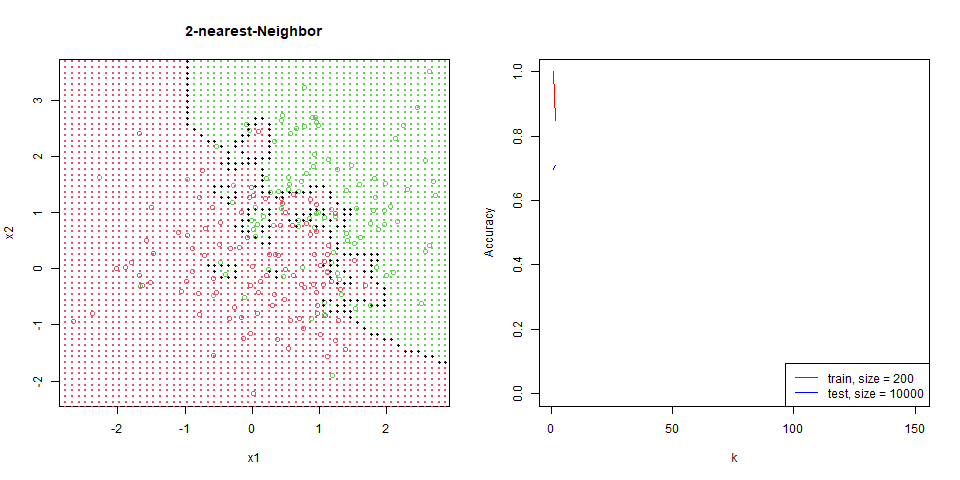
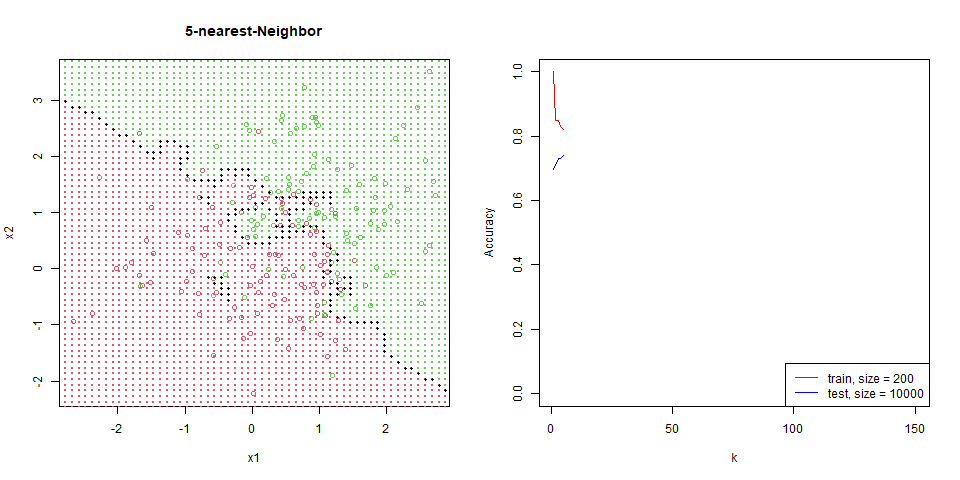
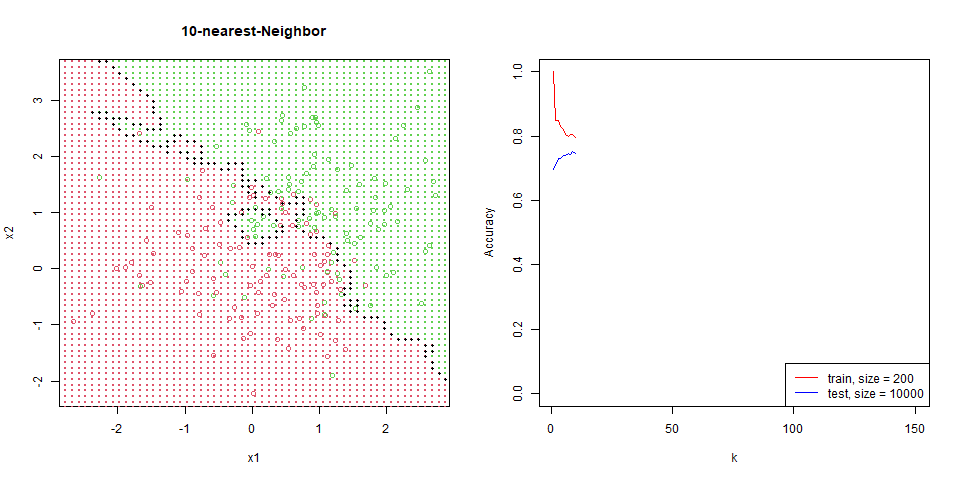
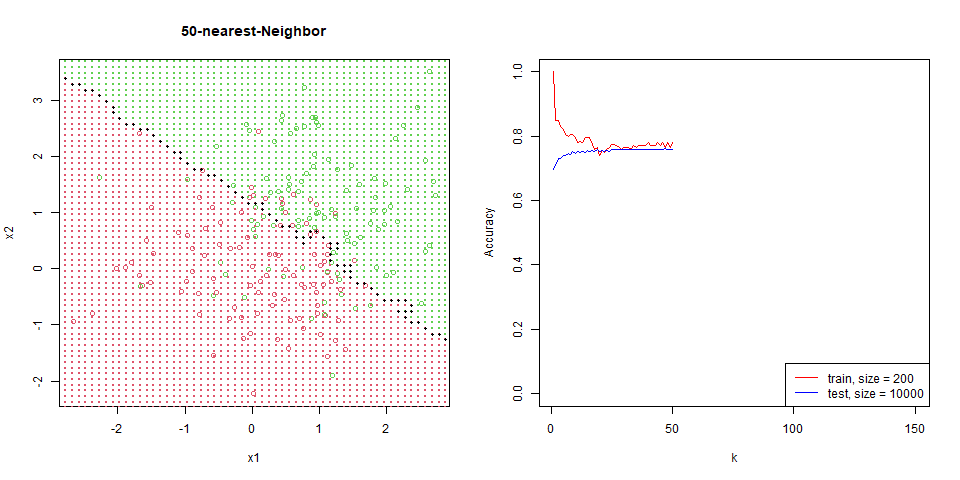
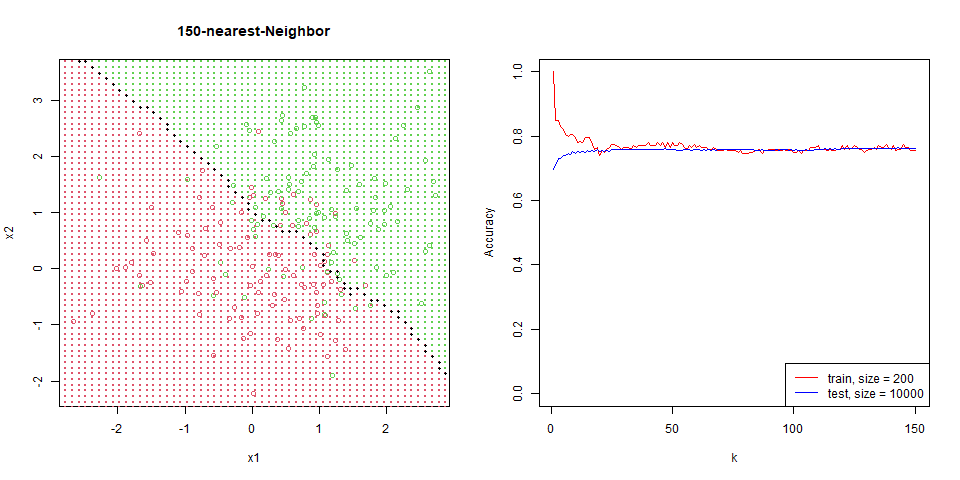
能看到隨著 增加,分區線逐漸變的平滑。
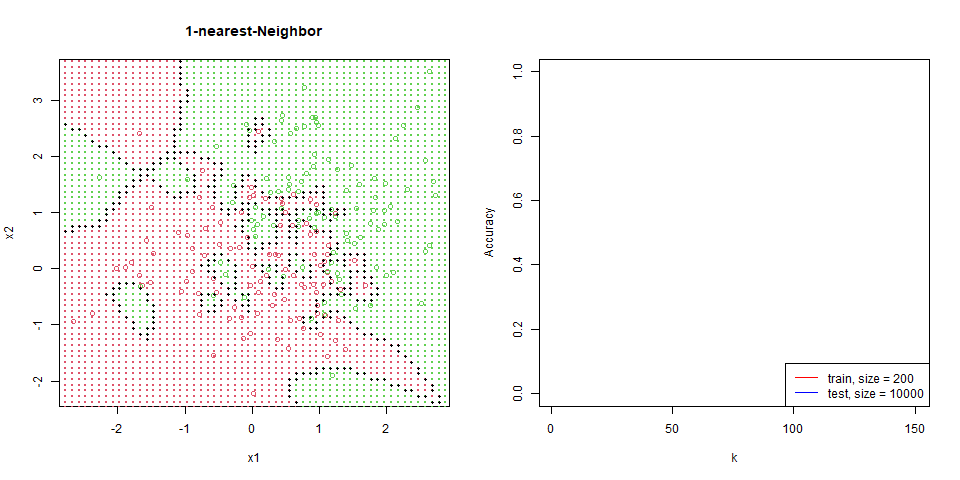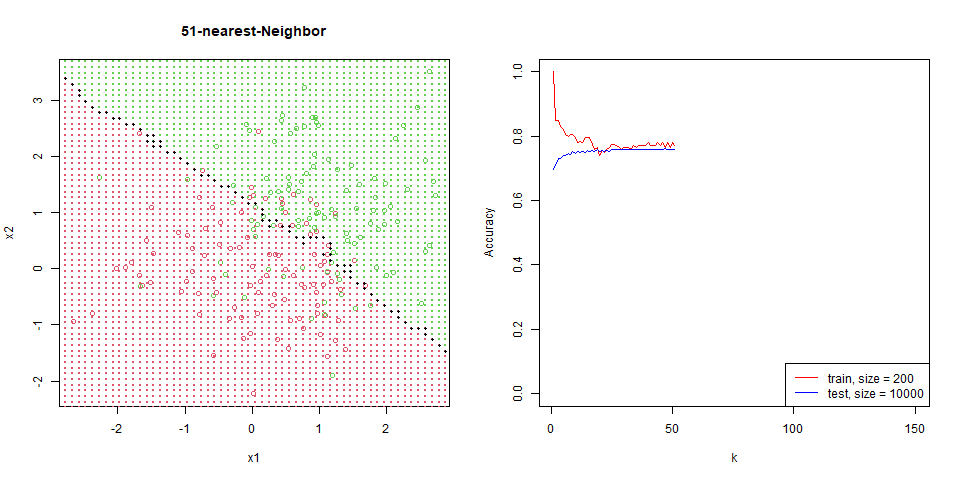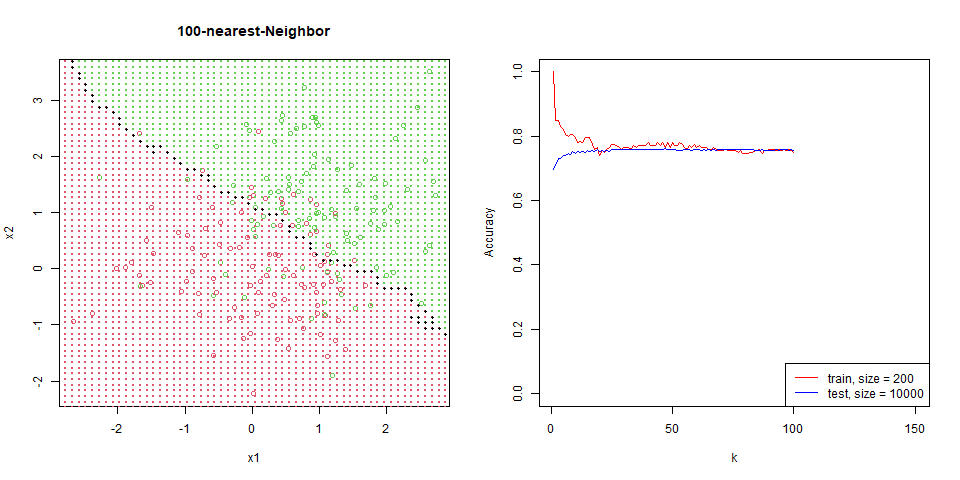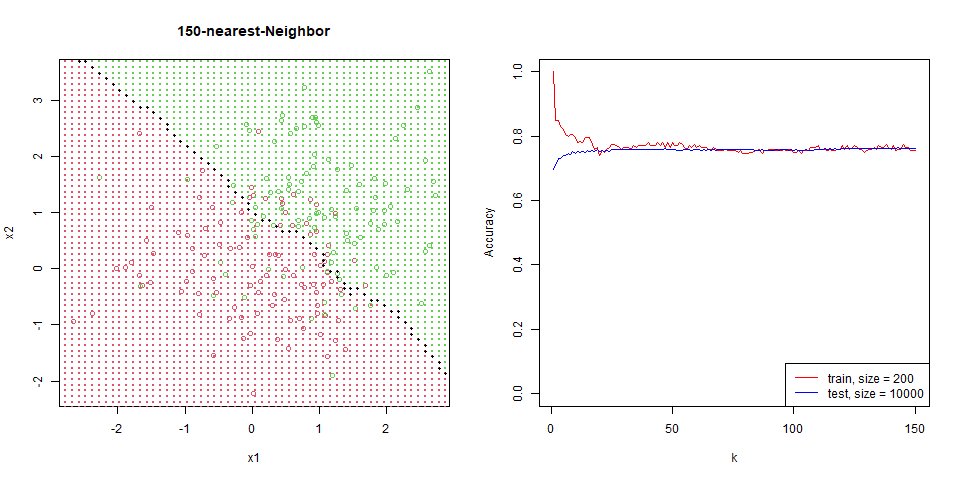
在這筆資料下的比對,能看出 regression 是非常穩定的,test 和 train 變化量並不大,而 knn 表現也逐漸趨於一致。
範例一 R 語言
給出範例一的程式。載入 packages
library(dplyr)
library(tidyverse)
library(MASS)
R分別生成出 train 和 test。
# generate data
n = 200 # train size
m = 10000 # test size
mu.0 = c(0, 0) # center of y 0
mu.1 = c(1, 1) # center of y 1
Sigma = matrix(c(1, 0, 0, 1), nrow = 2) # variance
set.seed(0) # random seed
# calculate
n.2 = n / 2
m.2 = m / 2
train = mvrnorm(n.2, mu = mu.0, Sigma = Sigma) %>%
rbind(mvrnorm(n.2, mu = mu.1, Sigma = Sigma)) %>%
cbind(y = c(rep(0, n.2), rep(1, n.2))) %>%
data.frame() %>%
rename(x1 = V1, x2 = V2)
test = mvrnorm(m.2, mu = mu.0, Sigma = Sigma) %>%
rbind(mvrnorm(m.2, mu = mu.1, Sigma = Sigma)) %>%
cbind(y = c(rep(0, m.2), rep(1, m.2))) %>%
data.frame() %>%
rename(x1 = V1, x2 = V2)
background = expand.grid(seq(-5, 5, length.out = 100),
seq(-5, 5, length.out = 100)) %>%
rename(x1 = Var1, x2 = Var2)
# plot
par(pty = "s")
plot(train$x1, train$x2, col = train$y + 2, xlab = "x1", ylab = "x2")
Rlinear regression 預測。
# linear regression
linear = lm(y ~ x1 + x2, train)
background$y = sapply(predict(linear, background), function(x){ if (x > 0.5) 1 else 0})
par(pty = "s")
plot(train$x1, train$x2, col = train$y + 2, xlab = "x1", ylab = "x2", main = "Linear Regression")
points(background$x1, background$x2, col = background$y + 2, pch = 19, cex = 0.1)
abline(a = (0.5 - linear$coefficients[1]) / linear$coefficients[3],
b = -linear$coefficients[2] / linear$coefficients[3])
# accuracy
linear.train = sapply(predict(linear, train), function(x){ if (x > 0.5) 1 else 0})
linear.train.acc = sum(linear.train == train$y) / n
linear.test = sapply(predict(linear, test), function(x){ if (x > 0.5) 1 else 0})
linear.test.acc = sum(linear.test == test$y) / m
Rknn 預測
# Nearest-Neighbor
library(FNN)
max.k = 150 # max k-near
train.acc = rep(NA, max.k)
test.acc = rep(NA, max.k)
for(k in 1:max.k){
if (k %% 10 == 0){ print(k) }
# calculate
background.knn = knn.reg(train = train[, 1:2], test = background[, 1:2], y = train[, 3], k = k)
background$y = sapply(background.knn$pred, function(x){ if (x > 0.5) 1 else 0})
train.knn = knn.reg(train = train[, 1:2], test = train[, 1:2], y = train[, 3], k = k)
train.pred = sapply(train.knn$pred, function(x){ if (x > 0.5) 1 else 0})
train.acc[k] = sum(train.pred == train$y) / n
test.knn = knn.reg(train = train[, 1:2], test = test[, 1:2], y = train[, 3], k = k)
test.pred = sapply(test.knn$pred, function(x){ if (x > 0.5) 1 else 0})
test.acc[k] = sum(test.pred == test$y) / m
# plot nearest-Neighbor
par(mfrow = c(1, 2))
plot(train$x1, train$x2, col = train$y + 2, xlab = "x1", ylab = "x2", main = paste0(k, "-nearest-Neighbor"))
points(background$x1, background$x2, col = background$y + 2, pch = 19, cex = 0.1)
# plot black dots
for(i in 1:100){
for(j in 1:99){
if(background[(i - 1) * 100 + j, 3] != background[(i - 1) * 100 + j + 1, 3]){
points(background[(i - 1) * 100 + j, 1:2], pch = 19, cex = 0.5)
}
if(background[(j - 1) * 100 + i, 3] != background[j * 100 + i, 3]){
points(background[(j - 1) * 100 + i, 1:2], pch = 19, cex = 0.5)
}
}
}
# plot Accuracy
plot(train.acc, ylim = c(0, 1), xlab = "k", ylab = "Accuracy", type = "l", col = "red")
points(test.acc, type = "l", col = "blue")
legend("bottomright",
c(paste0("train, size = ", n),
paste0("test, size = ", m)),
col = c("red", "blue"),
lty = 1)
}
R對比圖
# compare linear and knn
plot(train.acc, ylim = c(0, 1), xlab = "k", ylab = "Accuracy", type = "l", col = "red")
points(test.acc, type = "l", col = "blue")
abline(h = linear.train.acc, col = rgb(1, 0, 0, alpha = 0.5))
abline(h = linear.test.acc, col = rgb(0, 0, 1, alpha = 0.5))
legend("bottomright",
c(paste0("linear train, size = ", n),
paste0("linear test, size = ", m),
paste0("knn train, size = ", n),
paste0("knn test, size = ", m)),
col = c(rgb(1, 0, 0, alpha = 0.5), rgb(0, 0, 1, alpha = 0.5), "red", "blue"),
lty = 1)
R範例二
隨機生成資料中心點
- 組別一:
- 組別二:
每組再生成 100 筆資料,每筆資料有 的機率選擇組內 為中心,生成一個 ,第一組資料的 標記為 0 (紅色),第二組資料的 標記為 1 (綠色),圖中的實心點為 。
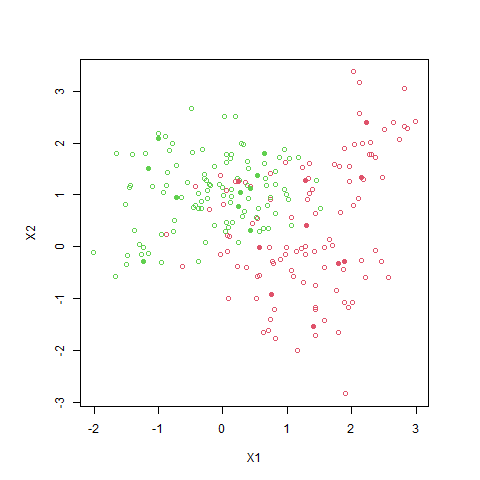
其 knn 的表現出
- train: 錯誤率隨著 在 150
10 的區間減少, 在 101 時的錯誤率減少的速度又更快。 - test: 錯誤率隨著 在 150
10 的區間減少,但 在 101 時的錯誤率又直線上升。
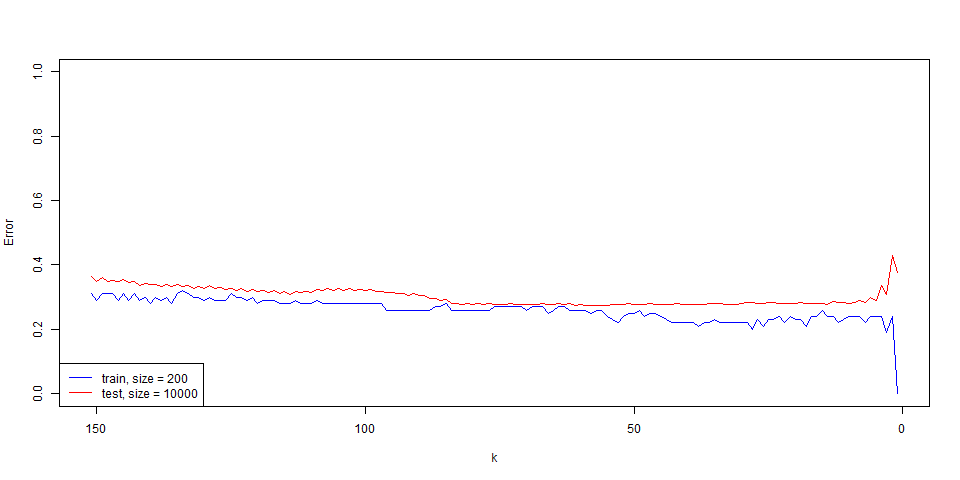
對 做 log 轉換
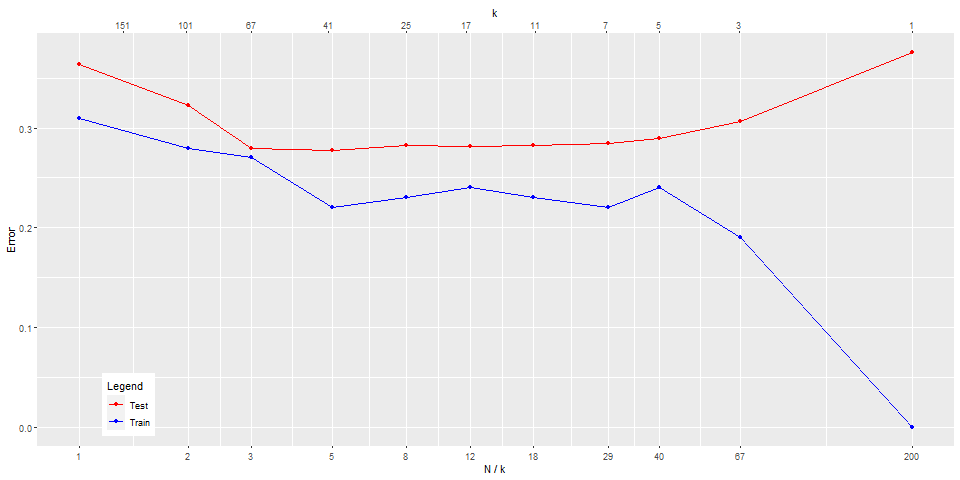
- 太小 () 會 over fitting。
- 在中間 () 表現較佳
- 從自由度 的角度更能看出變化趨勢。
範例二 R 語言
加載 package
library(dplyr)
library(tidyverse)
library(MASS)
R生成資料點的函式
# generate data
oracle = function(n, rand.seed = 1){
# oracle means
mu.0 = c(1, 0)
mu.1 = c(0, 1)
# class means
set.seed(0)
means.0 = mvrnorm(n = 10, mu = mu.0, Sigma = diag(2))
means.1 = mvrnorm(n = 10, mu = mu.1, Sigma = diag(2))
# observation
set.seed(rand.seed)
data.0 = sapply(1:n, function(i){
mvrnorm(1, mu = means.0[sample(1:10, 1), ], Sigma = diag(2) / 5)
}) %>% t() %>% data.frame() %>% cbind(y = 0)
data.1 = sapply(1:n, function(i){
mvrnorm(1, mu = means.1[sample(1:10, 1), ], Sigma = diag(2) / 5)
}) %>% t() %>% data.frame() %>% cbind(y = 1)
data = rbind(data.0, data.1)
}
R設定 sample size
# sample size for 1 class
train.size = 100
test.size = 5000
train = oracle(train.size)
test = oracle(test.size, rand.seed = 1234)
par(pty = 's')
plot(train[, 1:2], col = train$y + 2)
R執行 knn
# knn package
library(FNN)
max.k = 151 # max k-near
train.err = rep(NA, max.k)
test.err = rep(NA, max.k)
# calculate train and test error of each k
for(k in 1:max.k){
if (k %% 10 == 0){print(k)}
# for train part
train.knn = knn.reg(train = train[, 1:2], test = train[, 1:2], y = train[, 3], k = k)
train.pred = ifelse(train.knn$pred > 0.5, 1, 0)
train.err[k] = sum(train.pred != train$y) / train.size
# for test part
test.knn = knn.reg(train = train[, 1:2], test = test[, 1:2], y = train[, 3], k = k)
test.pred = ifelse(test.knn$pred > 0.5, 1, 0)
test.err[k] = sum(test.pred != test$y) / test.size
}
R畫出原始的 error 圖
# plot error
plot(train.err, ylim = c(0, 1), xlim = c(max.k, 1),
xlab = "k", ylab = "Error",
type = "l", col = "blue")
points(test.err, type = "l", col = "red")
legend("bottomleft",
c(paste0("train, size = ", train.size * 2),
paste0("test, size = ", test.size * 2)),
col = c("blue", "red"),
lty = 1)
R做 的轉換 error 圖
# plot error with transformation
library(ggplot2)
# plot breaks
Nk = c(1, 2, 3, 5, 8, 12, 18, 29, 40, 67, 200)
ks = c(151, 101, 67, 41, 25, 17, 11, 7, 5, 3, 1)
plot.err = data.frame(x = Nk, train = train.err[ks], test = test.err[ks])
ggplot(plot.err, aes(x = x)) +
geom_line(aes(y = train, color = "Train")) +
geom_point(aes(y = train, color = "Train")) +
geom_line(aes(y = test, color = "Test")) +
geom_point(aes(y = test, color = "Test")) +
scale_x_continuous(breaks = Nk, trans = "log10",
sec.axis = sec_axis(~200/., breaks = ks, name = "k") ) +
labs(x = "N / k", y = "Error") +
scale_color_manual(values = c("red", "blue"), name = "Legend", labels = c("Test", "Train")) +
theme(legend.position = c(0.1, 0.1)) # 圖例位置
R沒有白吃的午餐定理 (No Free Lunch Theorem)
下面兩張圖分別是對應不同資料集的模型精確度,能看出圖一選擇線性回歸,圖二選擇小 的近鄰演算法可能是較好的選項。


上述案例中能看出,沒有一種機器學習能夠在所有問題上表現最好,又稱為 沒有白吃的午餐定理 (No Free Lunch Theorem),可以想像成沒有一種午餐能滿足所有人。因此機器學習沒有通用的最佳解,需要根據問題與資料選模型。
統計決策理論 (Statistical Decision Theory)
決策理論告訴我們「一個模型能達到的最好程度」。舉例來說,若母體取樣來自各半的 與 。若採樣的 ,則 可以保證來自 ;相似的,若採樣的 ,則 可以保證來自 ;若 ,則說 來自 或 都僅有一半的正確率,因此在此問題下能達到的最好正確率只有75%。實際問題中,不知道背後真實的母體分配,因此會靠重抽 (boosting) 等方式來模擬母體的分配。
現假設 是連續型變數,要刻劃模型的適配程度,首先定義 loss function (損失函數)
目標是要最小化損失,因此定義 expected (squared) prediction error,同時也是 Bayes risk
而在 squared loss function 底下,最小化 EPE 可以寫成
這樣的 也被稱之為 regression function (回歸函數),意指在給定 條件下, 最有可能的數值。而在 是類別型變數時,則會改取眾數