線性回歸診斷與治療 (Diagnostic and Remedial)

診斷與治療 (Diagnostic and Remedial)

要確定模型是否合適，須檢驗模型的前提，即常態假設 $\contia{\varepsilon}{n} \iid N (0, \sigma^2)$，但實際上 $\varepsilon_i$ 是未知的，因此會用殘差項 $e_i$ 估計 $\varepsilon_i$

前面的範例中能看到 $R^2$ 高達 $0.9$ 但卻不是適合的模型，原因就是其殘差違反常態假設。

建立模型後需檢驗殘差是否滿足常態假設，因為 $t$ 檢定、$F$ 檢定與各種顯著性檢定是基於常態假設所做的推論，若常態假設被違反，各種推論都是不可信的。

特別注意 $e_i$ 並非獨立的隨機變數，因為計算 $b_0$ 與 $b_1$ 涉及到所有 $Y$。但若常態假設成立，$e_i \approx N (0, \sigma^2)$，多數情況下非獨立的影響可以忽略不計。而我們的目標是要驗證

1. 模型是否合理：$E (\hat Y) = E (Y)$
2. 殘差是否常態：$e_i \approx N (0, \sigma^2)$
   1. $E (e_i) \approx 0$
   2. $\sigma^2 (e_i) \approx \sigma^2$
   3. $\sigma (e_i, e_j) \approx 0$

模型合理性

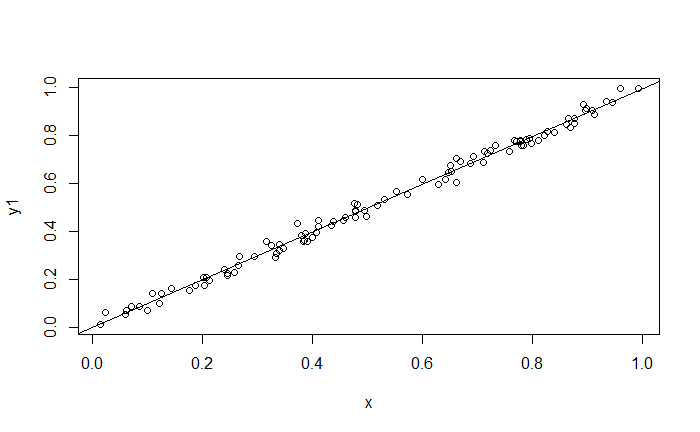
檢查 $X$ 對 $Y$ 的圖，理想上該看到 $X$ 與 $Y$ 呈現現性關係

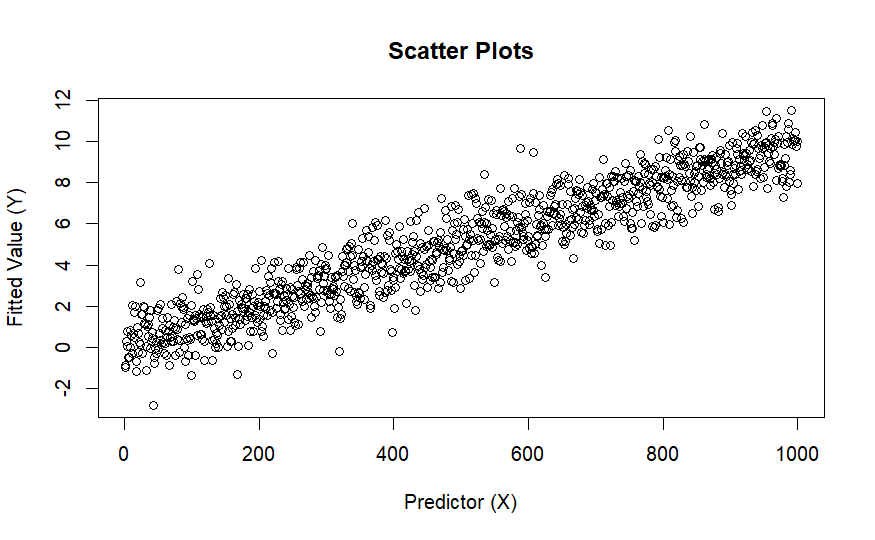
而非下圖

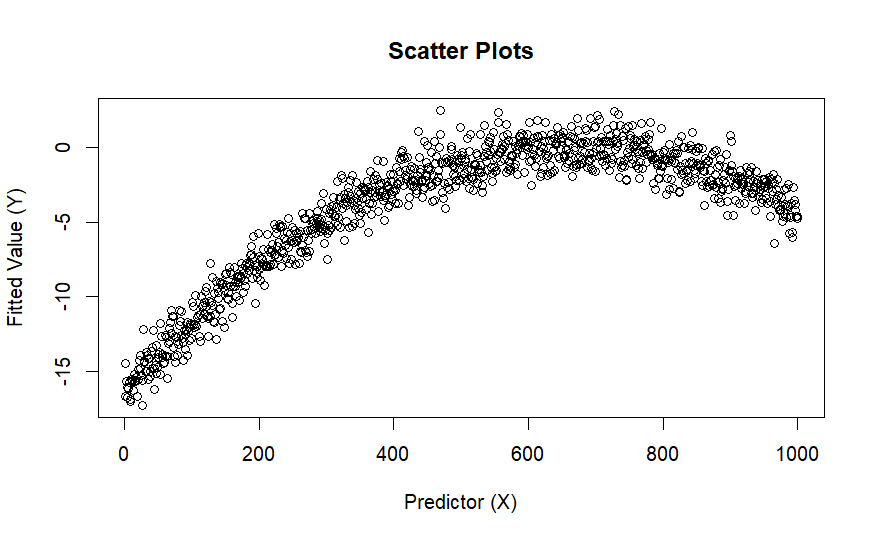
解決方案：考慮不同回歸模型 $Y_i = \beta_0 + \beta_1 Z_i + \varepsilon_i$，例如 $Z_i = X_i^2$

影響點 (Influence Points)

影響點 (Influence Points) 指的是會嚴重帶偏模型的點，發生在遠離群集的點，被稱為異常點 (outlier)

影響點是一種異常點，但異常點不一定是影響點

用紅點將異常點畫出，下圖的異常點僅稍微影響斜率，但對模型影響不大

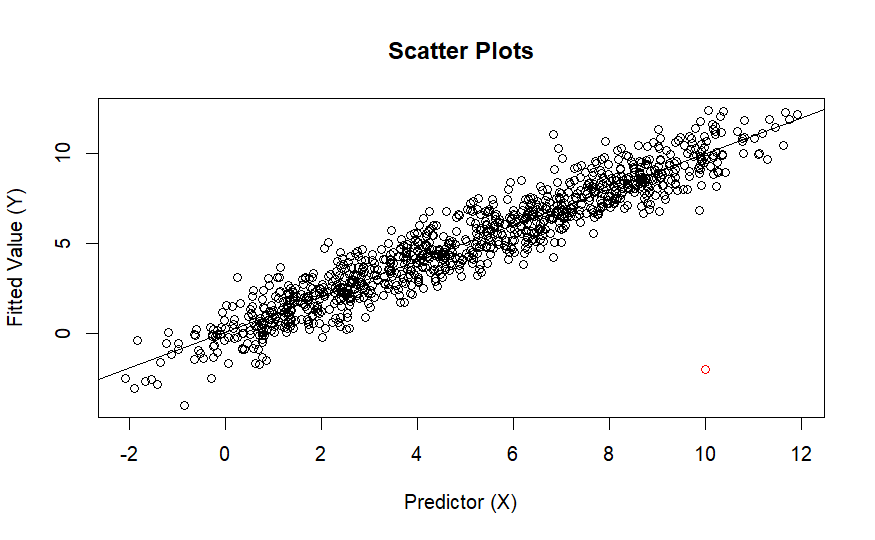
而下圖的異常點的影響力大到將模型的正負號改變

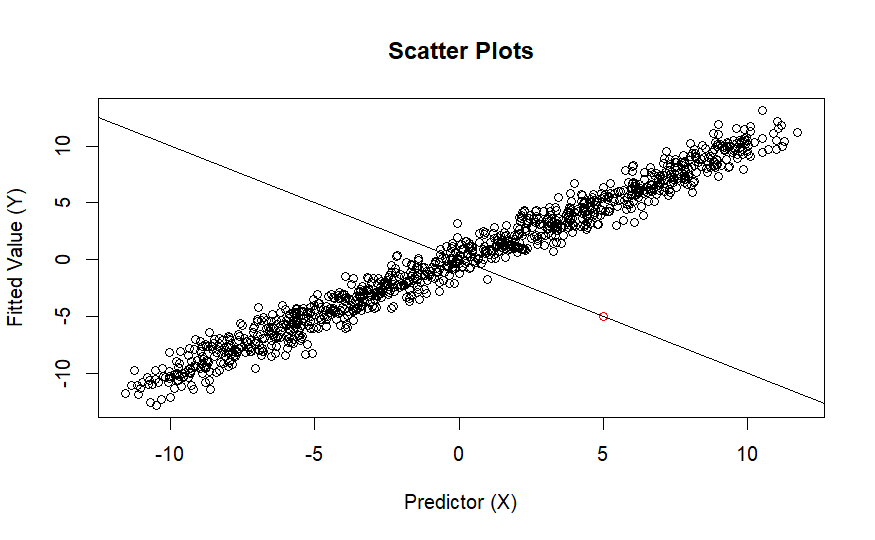
最後一種是，多數的點並沒有線性關係，但異常點卻影響了整條斜率

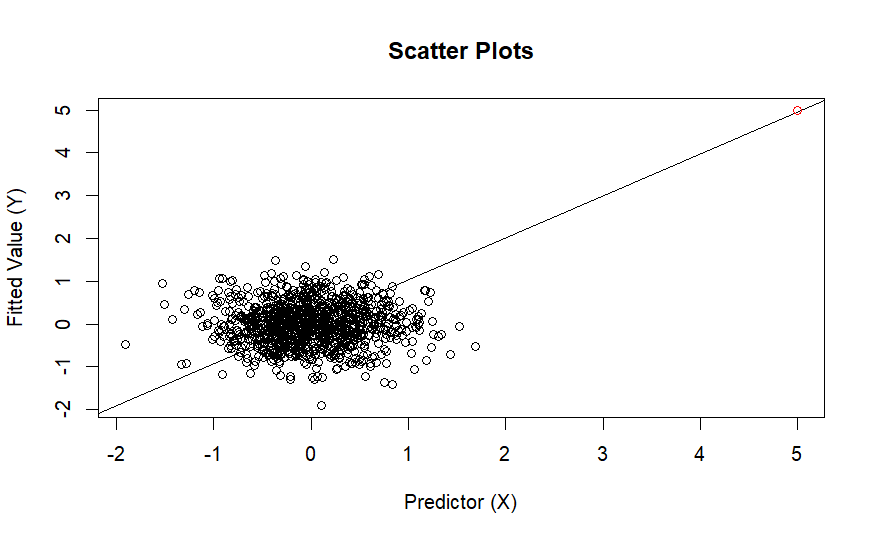
解決方案：檢查異常點的來源，僅在能確定是錯誤的前提下，才將異常點移除。

殘差常態檢驗

需檢驗的項目

1. 殘差直方圖 (histogram)
2. 殘差時間序列圖 (time sequence plot, $i$ 對 $e_i$)
3. 殘差對 ($X_i$ 對 $e_i$)
4. 殘差對預測值 ($\hat Y_i$ 對 $e_i$)

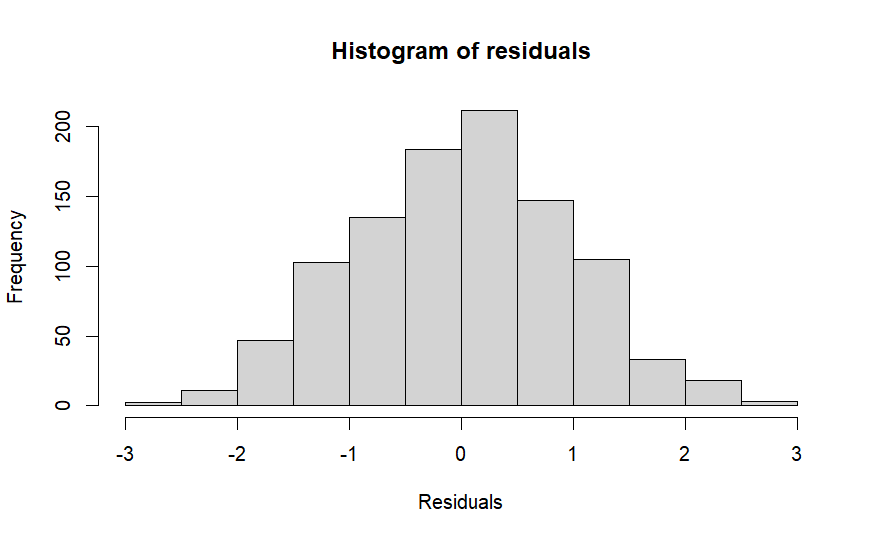
殘差直方圖 (Histogram)

下圖理想的殘差直方圖 (histogram)，其呈現常態的模式

殘差時間序列圖 (time sequence plot, $i$ 對 $e_i$)

R 語言程式範例

參考資料

1. 書籍：Applied linear statistical models. NETER, John, et al. 1996.
2. 網站：Stat 501