☰

圓州率
🌐
☰

Feature Image

Latent Dirichlet Allocation (LDA) 理論

數學, 資料科學, 機器學習, 文字探勘, 非監督式學習, Latent Dirichlet Allocation (LDA)
透過層次結構來執行自然語言處理 (Natural Language Processing)，介紹 Latent Dirichlet Allocation。
   最後更新:

介紹

Latent dirichlet allocation (LDA) 一種常用於文字探勘的非監督式機器學習，目標是將大量文件 (documents)，依據其使用單字 (words) 頻率，為其生成主題分佈 (topics)，以此達成文件分類，是 latent semantic analysis (LSA) 的擴展模型，連結的文章會介紹 LDA 應用。

LSA 假設

  1. 每個文件 (document) 是主題 (topics) 的 multinomial 分佈，稱為主題分佈
  2. 每個主題 (topics) 是單字 (words) 的 multinomial 分佈，稱為單字分佈

其中主題分佈與單字分佈都是未知的，僅有文件的用字頻率是已知的；而 LDA 引入 Dirichlet distribution，作為主題分佈與單字分佈的先驗 (prior) 分佈。

分配

Multinomial Distribution

假設有 kk 種可能的輸出，第 ii 種輸出的機率為 pi≥0p_i \geq 0，且 ∑i=1kpi=1\sum_{i = 1}^{k} p_i = 1，對應的出現次數為 xix_i，則隨機變數 X~=(X1,X2,⋯ ,Xk)\ut X = (\contia{X}{k}) 有以下 PDF，

P(X~=x~∣n,p~)=n!∏i=1k(xi)!∏i=1kpixi \begin{align*} P (\ut X = \ut x | n, \ut p) & = \frac{n!}{\prod_{i = 1}^{k} (x_i)!} \prod_{i = 1}^{k} p_i^{x_i} \end{align*}

其中 ∑i=1kxi=n\sum_{i = 1}^{k} x_i = n，且 xi∈Nx_i \in \bb N (>0> 0)，寫作 X~∼Mult(n,p~)\ut X \sim \text{Mult} (n, \ut p)；若 n=1n = 1 時，簡寫為 Mult(p~)\text{Mult} (\ut p)。

Dirichlet Distribution

Dirichlet distribution 是 beta distribution 的擴展版，或稱 multivariate beta distribution。給定參數 α~=(α1,α2,⋯ ,αk)\ut \alpha = (\contia{\alpha}{k})，αi>0\alpha_i > 0 對任意 i=1,2,⋯ ,ki = \conti{k}，則隨機變數 θ~=(θ1,θ2,⋯ ,θk)\ut \theta = (\contia{\theta}{k}) 有以下 PDF，

P(θ~∣α~)=Γ(∑i=1kαi)∏i=1kΓ(αi)∏i=1kθiαi−1 \begin{align*} P (\ut \theta | \ut \alpha) & = \frac{\Gamma (\sum_{i = 1}^{k} \alpha_i)}{\prod_{i = 1}^{k} \Gamma (\alpha_i)} \prod_{i = 1}^{k} \theta_i^{\alpha_i - 1} \end{align*}

其中 ∑i=1kθi=1\sum_{i = 1}^{k} \theta_i = 1，且 θi≥0\theta_i \geq 0 對任意 i=1,2,⋯ ,ki = \conti{k}，寫作 θ~∼Dir(α~)\ut \theta \sim \text{Dir} (\ut \alpha)。

Properties

Γ(s)\Gamma (s) 是 gamma function，定義 multivariate beta function

B(α~)=∏i=1kΓ(αi)Γ(∑i=1kαi) \begin{align*} B (\ut \alpha) & = \frac{\prod_{i = 1}^{k} \Gamma (\alpha_i)}{\Gamma (\sum_{i = 1}^{k} \alpha_i)} \end{align*}

使得 Dirichlet distribution 的 PDF 寫成

P(θ~∣α~)=1B(α~)∏i=1kθiαi−1 \begin{align*} P (\ut \theta | \ut \alpha) & = \frac{1}{B (\ut \alpha)} \prod_{i = 1}^{k} \theta_i^{\alpha_i - 1} \end{align*}

因 PDF 的性質

1=∫P(θ~∣α~)dθ~=1B(α~)∫∏i=1kθiαi−1dθ~ \begin{align*} 1 = \int P (\ut \theta | \ut \alpha) d \ut \theta = \frac{1}{B (\ut \alpha)} \int \prod_{i = 1}^{k} \theta_i^{\alpha_i - 1} d \ut \theta \end{align*}

所以

B(α~)=∫∏i=1kθiαi−1dθ~ \begin{align*} B (\ut \alpha) = \int \prod_{i = 1}^{k} \theta_i^{\alpha_i - 1} d \ut \theta \end{align*}

Conjugate Prior

基於 Bayes' theorem

p(θ∣x)⏟posterior=p(θ)⏟prior×p(x∣θ)⏟likehood÷p(x)⏟marginal=p(θ)p(x∣θ)∫p(θ)p(x∣θ)dθ∝p(θ)p(x∣θ) \begin{align*} \underbrace{p (\theta | x)}_{\text{posterior}} & = \underbrace{p (\theta)}_{\text{prior}} \times \underbrace{p (x | \theta)}_{\text{likehood}} \div \underbrace{p (x)}_{\text{marginal}} \\ & = \frac{p (\theta) p (x | \theta)}{\int p (\theta) p (x | \theta) d \theta} \\ & \propto p (\theta) p (x | \theta) \end{align*}

若 prior p(θ)p (\theta) 和 posterior p(θ∣x)p (\theta | x) 是相同類型的分佈，則稱此 prior 為 conjugate prior，而選用 conjugate distribution 能較容易從 prior 計算 posterior。

給定 X~∼Mult(n,θ~)\ut X \sim \text{Mult} (n, \ut \theta)，其中參數的 prior 為 θ~∼Dir(α~)\ut \theta \sim \text{Dir} (\ut \alpha)，則 posterior 為

p(θ~∣x~,α~)∝p(θ~∣α~)p(x~∣θ~)=[1B(α~)∏i=1kθiαi−1][n!∏i=1k(xi!)∏i=1kθixi]∝∏i=1kθiαi+xi−1 \begin{align*} p (\ut \theta | \ut x, \ut \alpha) & \propto p (\ut \theta | \ut \alpha) p (\ut x | \ut \theta) \\ & = \left[ \frac{1}{B (\ut \alpha)} \prod_{i = 1}^{k} \theta_i^{\alpha_i - 1} \right] \left[ \frac{n!}{\prod_{i = 1}^{k} (x_i!)} \prod_{i = 1}^{k} \theta_i^{x_i} \right] \\ & \propto \prod_{i = 1}^{k} \theta_i^{\alpha_i + x_i - 1} \end{align*}

即 θ∣x~,α~∼Dir(x~+α~)\theta | \ut x, \ut \alpha \sim \text{Dir} (\ut x + \ut \alpha)，因此 Dirichlet 為 Multinomial 的 conjugate prior。

模型定義

簡化模型

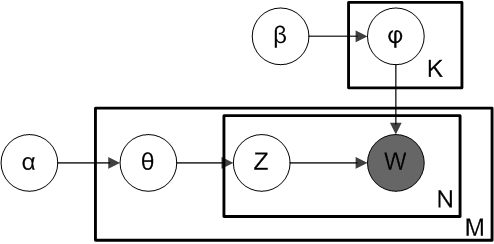
給定 KK 個主題、VV 種單字、參數 α~∈RK\ut \alpha \in \bb R^{K} 和 β~∈RV\ut \beta \in \bb R^{V}，LDA 假設一份 NN 字的文件生成為順序為

  1. 生成每個主題下的單字分佈 φk~∼Dir(β~)\ut {\varphi_k} \sim \text{Dir} (\ut \beta) 對 k=1,2,⋯ ,Kk = \conti{K}。
  2. 生成文件下的主題分佈 θ~∼Dir(α~)\ut {\theta} \sim \text{Dir} (\ut \alpha)。
  3. 生成文件下的單字
    1. 選定每個位置下的主題 zn∼Mult(θ~)z_n \sim \text{Mult} (\ut \theta)，對 n=1,2,⋯ ,Nn = \conti{N}。
    2. 選定每個位置下的單字 wn∼Mult(φzn~)w_n \sim \text{Mult} (\ut {\varphi_{z_n}})，對 n=1,2,⋯ ,Nn = \conti{N}。

範例

例如2個主題、100100個單字、參數 α=(2,1)\alpha = (2, 1) 表示為 (數學、體育) 和 β=(2,2,0.1,2,2,⋯ )\beta = (2, 2, 0.1, 2, 2, \cdots) 表示為 (數字、函數、共軛、勝率、運動)，則一份10個字的文件生成順序如下

  1. 生成每個主題下的單字分佈
    • 例如主題1 φ1~=(0.4,0.4,0.08,0.01,0.01,⋯ )\ut {\varphi_1} = (0.4, 0.4, 0.08, 0.01, 0.01, \cdots)，常用字為數字、函數、共軛
    • 例如主題2 φ2~=(0.08,0.01,0.01,0.4,0.4,⋯ )\ut {\varphi_2} = (0.08, 0.01, 0.01, 0.4, 0.4, \cdots)，常用字為勝率、運動
  2. 生成文件下的主題分佈
    • 例如偏向數學主題 θ~=(0.9,0.1)\ut \theta = (0.9, 0.1)
  3. 生成文件下的單字
    • 因 ϕ\phi 偏第1維度，Mult(θ~)\text{Mult} (\ut \theta) 採樣結果容易為1，而不容易為2；假設 z1=z2=⋯=z9=1z_1 = z_2 = \cdots = z_9 = 1，z10=2z_{10} = 2。
    • 生成第1個字，w1∼Mult(φz1~)=Mult(φ1~)w_1 \sim \text{Mult} (\ut {\varphi_{z_1}}) = \text{Mult} (\ut {\varphi_1}) 容易出現數字、函數、共軛等字
    • 生成第2個字，w2∼Mult(φz2~)=Mult(φ1~)w_2 \sim \text{Mult} (\ut {\varphi_{z_2}}) = \text{Mult} (\ut {\varphi_1}) 容易出現數字、函數、共軛等字
    • ⋮\vdots
    • 生成第10個字，w10∼Mult(φz10~)=Mult(φ2~)w_{10} \sim \text{Mult} (\ut {\varphi_{z_{10}}}) = \text{Mult} (\ut {\varphi_2}) 容易出現勝率、運動

在此範例中能看出，φ1~\ut{\varphi_1} 與 φ2~\ut{\varphi_2} 決定每個主題下的常用字。

完整模型

LDA 假設 KK 是已知的，實務上透過實驗選擇出來，某些實驗結果表明 20 種主題已經足夠；α~\ut \alpha 與 β~\ut \beta 若無先驗知識的情況下，建議將 α~\ut \alpha 與 β~\ut \beta 的所有分量均設為1。現在考慮 KK 個主題、VV 種單字、MM 份文件，文件字數分別為 (N1,N2,⋯ ,NM)(\contia{N}{M}) 則 LDA 的生成順序為

  1. 生成每個主題下的單字分佈 φk~∼Dir(β~)\ut {\varphi_k} \sim \text{Dir} (\ut \beta) 對 k=1,2,⋯ ,Kk = \conti{K}。
  2. 生成每份文件下的主題分佈 θm~∼Dir(α~)\ut {\theta_m} \sim \text{Dir} (\ut \alpha) 對 m=1,2,⋯ ,Mm = \conti{M}。
  3. 生成文件下的單字
    1. 選定每個位置下的主題 zmn∼Mult(θm~)z_{mn} \sim \text{Mult} (\ut {\theta_m})，對 m=1,2,⋯ ,Mm = \conti{M} 與 n=N1,N2,⋯ ,Nmn = \contia{N}{m}
    2. 選定每個位置下的單字 wmn∼Mult(φzmn~)w_{mn} \sim \text{Mult} (\ut {\varphi_{z_{mn}}})，對 m=1,2,⋯ ,Mm = \conti{M} 與 n=N1,N2,⋯ ,Nmn = \contia{N}{m}

其中 φk~\ut {\varphi_k} 決定每個主題下的單字分佈，θm~\ut {\theta_m} 決定每個文件的主題分佈。現在簡化符號

  1. 以 φ={φk~}k=1K∈RK×V\bs \varphi = \{\ut {\varphi_k}\}_{k = 1}^{K} \in \bb R^{K \times V} 表示單字分佈矩陣
  2. 以 θ={θm~}m=1M∈RM×K\bs \theta = \{\ut {\theta_m}\}_{m = 1}^{M} \in \bb R^{M \times K} 表示主題分佈矩陣
  3. 以 z={zm~}m=1M\bs z = \{\ut {z_m}\}_{m = 1}^{M} 表示主題矩陣
  4. 以 w={wm~}m=1M\bs w = \{\ut {w_m}\}_{m = 1}^{M} 表示單字矩陣

則給定參數 α\alpha 與 β\beta 後，完整的機率模型可以被表示為 mm 份文件的機率相乘

p(w,z,θ,φ∣α~,β~)=∏k=1Kp(φk~∣β~)∏m=1Mp(θm~∣α~)∏n=1Nmp(zmn∣θm~)p(wmn∣φzmn~)=∏m=1Mp(wm~,zm~,θm~,φ∣α~,β~) \begin{align*} p (\bs w, \bs z, \bs \theta, \bs \varphi | \ut \alpha, \ut \beta) & = \prod_{k = 1}^{K} p (\ut {\varphi_k} | \ut \beta) \prod_{m = 1}^{M} p (\ut {\theta_m} | \ut \alpha) \prod_{n = 1}^{N_m} p (z_{mn} | \ut {\theta_m}) p (w_{mn} | \ut {\varphi_{z_{mn}}}) \\ & = \prod_{m = 1}^{M} p (\ut {w_m}, \ut {z_m}, \ut {\theta_m}, \bs \varphi | \ut \alpha, \ut \beta) \end{align*}

其中第 mm 份文件的機率為

p(wm~,zm~,θm~,φ∣α~,β~)=∏k=1Kp(φk~∣β~)p(θm~∣α~)∏n=1Nmp(zmn∣θm~)p(wmn∣φzmn~) \begin{align*} p (\ut {w_m}, \ut {z_m}, \ut {\theta_m}, \bs \varphi | \ut \alpha, \ut \beta) & = \prod_{k = 1}^{K} p (\ut {\varphi_k} | \ut \beta) p(\ut {\theta_m} | \ut \alpha) \prod_{n = 1}^{N_m} p (z_{mn} | \ut {\theta_m}) p (w_{mn} | \ut {\varphi_{z_{mn}}}) \end{align*}

前半部的 p(φk~∣β~)p(θm~∣α~)p (\ut {\varphi_k} | \ut \beta) p(\ut {\theta_m} | \ut \alpha) 為兩個獨立的 Dirichlet 機率，後半部的 p(zmn∣θm~)p(wmn∣φzmn~)p (z_{mn} | \ut {\theta_m}) p (w_{mn} | \ut {\varphi_{z_{mn}}}) 為兩步驟的 Multinomial 機率，然而 z\bs z 是未知的，僅有觀測到 w\bs w，因此轉而計算 (wm~∣θm~,φ)(\ut {w_m} | \ut {\theta_m}, \bs \varphi) 的 marginal PDF

p(wm~∣θm~,φ)=∑k=1K[∏n=1Nmp(zmn∣θm~)p(wmn∣φzmn~)|zmn=k]=∏n=1Nm[∑k=1Kp(zmn=k∣θm~)p(wmn∣φk~)] \begin{align*} p (\ut {w_m} | \ut {\theta_m}, \bs \varphi) & = \sum_{k = 1}^{K} \left[ \prod_{n = 1}^{N_m} p (z_{mn} | \ut {\theta_m}) p (w_{mn} | \ut {\varphi_{z_{mn}}}) \middle| z_{mn} = k \right] \\ & = \prod_{n = 1}^{N_m} \left[ \sum_{k = 1}^{K} p (z_{mn} = k| \ut {\theta_m}) p (w_{mn} | \ut {\varphi_k}) \right] \end{align*}

然而 θ\bs \theta 與 φ\bs \varphi 也仍然是未知的。再次計算條件機率，即可計算出給定 prior 參數 α~\ut \alpha 與 β~\ut \beta 下，每份文件出現的機率

p(wm~∣α~,β~)=∏k=1K∫∫p(φk~∣β~)p(θm~∣α~)p(wm~∣θm~,φ)dθm~dφk~ \begin{align*} p (\ut {w_m} | \ut \alpha, \ut \beta) & = \prod_{k = 1}^{K} \int \int p (\ut {\varphi_k} | \ut \beta) p (\ut {\theta_m} | \ut \alpha) p (\ut {w_m} | \ut {\theta_m}, \bs \varphi) d \ut {\theta_m} d \ut {\varphi_k} \end{align*}

所有文件的 joint PDF 為

p(w∣α~,β~)=∏m=1Mp(wm~∣α~,β~) \begin{align*} p (\bs w | \ut \alpha, \ut \beta) = \prod_{m = 1}^{M} p (\ut {w_m} | \ut \alpha, \ut \beta) \end{align*}

參數估計

機率模型中包含3個隱藏參數 z\bs z (每個單字的主題)、θ\bs \theta (主題分佈) 與 φ\bs \varphi (單字分佈) 是估計目標，從 z\bs z 開始。考慮第1份文件，以 w,z,φ,θw, z, \varphi, \theta 表示 第一份文件對應的 w1~,z1~,φ1~,θ1~\ut {w_1}, \ut {z_1}, \ut {\varphi_1}, \ut {\theta_1} ，在給定文件與參數下，每個單字的主題分佈機率如下

p(z∣w,α~,β~)=p(w,z∣α~,β~)p(w∣α~,β~) \begin{align*} p (z | w, \ut \alpha, \ut \beta) = \frac{p (w, z | \ut \alpha, \ut \beta)}{p (w | \ut \alpha, \ut \beta)} \end{align*}

分母的部分已知，而分子可以拆分為兩部分

p(w,z∣α~,β~)=p(w∣z,α~,β~)p(z∣α~,β~)=p(w∣z,β~)p(z∣α~) \begin{align*} p (w, z | \ut \alpha, \ut \beta) & = p (w | z, \ut \alpha, \ut \beta) p (z | \ut \alpha, \ut \beta) \\ & = p (w | z, \ut \beta) p (z |\ut \alpha) \end{align*}

先處理第一部分，令 φkv\varphi_{kv} 為第 kk 個主題下，第 vv 個單字的機率，令nkvn_{kv} 為第 kk 個主題下，第 vv 個字出現的次數，且 nk={nk1,nk2,⋯ ,nkV}n_k = \{ n_{k1}, n_{k2}, \cdots, n_{kV} \}

p(w∣z,β~)=∫p(w∣z,φ)p(φ,β~)dφ=∫[∏k=1K∏v=1Vφkvnkv][1B(β~)∏v=1Vφkvβv−1]dφ=∏k=1K1B(β~)∫∏v=1Vφkvnkv+βv−1dφ=∏k=1KB(nk~+β~)B(β~) \begin{align*} p (w | z, \ut \beta) & = \int p (w | z, \varphi) p (\varphi, \ut \beta) d \varphi \\ & = \int \left[ \prod_{k = 1}^{K} \prod_{v = 1}^{V} \varphi_{kv}^{n_{kv}} \right] \left[ \frac{1}{B (\ut \beta)} \prod_{v = 1}^{V} \varphi_{k_v}^{\beta_v - 1} \right] d \varphi \\ & = \prod_{k = 1}^{K} \frac{1}{B (\ut \beta)} \int \prod_{v = 1}^{V} \varphi_{kv}^{n_{kv} + \beta_v - 1} d \varphi \\ & = \prod_{k = 1}^{K} \frac{B (\ut {n_k} + \ut \beta)}{B (\ut \beta)} \end{align*}

相似的，令 nmkn_{mk} 為第 mm 篇文件下，第 kk 個主題出現的次數，且 nm={nm1,nm2,⋯ ,nmK}n_m = \{ n_{m1}, n_{m2}, \cdots, n_{mK} \}

p(z∣α~)=∫p(z∣θ)p(θ,α~)dθ=∏m=1MB(nm~+α~)B(α~) \begin{align*} p (z | \ut \alpha) & = \int p (z | \theta) p (\theta, \ut \alpha) d \theta \\ & = \prod_{m = 1}^{M} \frac{B (\ut {n_m} + \ut \alpha)}{B (\ut \alpha)} \end{align*}

綜合上式，可獲得

p(w,z∣α~,β~)=∏k=1KB(nk~+β~)B(β~)∏m=1MB(nm~+α~)B(α~) \begin{align*} p (w, z | \ut \alpha, \ut \beta) = \prod_{k = 1}^{K} \frac{B (\ut {n_k} + \ut \beta)}{B (\ut \beta)} \prod_{m = 1}^{M} \frac{B (\ut {n_m} + \ut \alpha)}{B (\ut \alpha)} \end{align*}

使得

p(z∣w,α~,β~)=1p(w∣α~,β~)∏k=1KB(nk~+β~)B(β~)∏m=1MB(nm~+α~)B(α~) \begin{align*} p (z | w, \ut \alpha, \ut \beta) = \frac{1}{p (w | \ut \alpha, \ut \beta)} \prod_{k = 1}^{K} \frac{B (\ut {n_k} + \ut \beta)}{B (\ut \beta)} \prod_{m = 1}^{M} \frac{B (\ut {n_m} + \ut \alpha)}{B (\ut \alpha)} \end{align*}

不過其中的 nk~\ut {n_k} 與 nm~\ut {n_m} 是未知的，可以透過 Gibbs sampling 與下列式估計

P(zi=k∣z−i,w,α,β)∝nkv+βv∑v=1V(nkv+βv)⋅nmk+αk∑k=1K(nmk+αk) \begin{align*} P (z_i = k | \bs z_{-i}, w, \alpha, \beta) \propto \frac{n_{kv} + \beta_v}{\sum_{v = 1}^{V} (n_{kv} + \beta_v)} \cdot \frac{n_{mk} + \alpha_k}{\sum_{k = 1}^{K} (n_{mk} + \alpha_k)} \end{align*}

參考資料

  1. LI, Hang. Machine Learning Methods. Springer Nature, 2023.

勘誤

這篇文章帶有一定量的錯誤，我會列出有錯誤的式子，紅色是錯誤，綠色是修正

p(θ∣α)=Γ(∑i=1kαi)∏i=1kΓ(α)k∏i=1kθiαi−1p(θ∣α)=Γ(∑i=1kαi)∏i=1kΓ(α)∏i=1kθiαi−1 \begin{align} \tag{20.2} p (\theta | \alpha) = \frac{\Gamma \left( \sum_{i = 1}^{k} \alpha_i \right)}{\prod_{i = 1}^{k} \Gamma (\alpha)^{\color{red}{k}}} \prod_{i = 1}^{k} \theta_i^{\alpha_i - 1} \\ \notag p (\theta | \alpha) = \frac{\Gamma \left( \sum_{i = 1}^{k} \alpha_i \right)}{\prod_{i = 1}^{k} \Gamma (\alpha)} \prod_{i = 1}^{k} \theta_i^{\alpha_i - 1} \end{align} p(wm,zm,θm,φ∣α,β)=∏k=1Kp(ϕk∣β)p(θm∣α)∏m=1Nmp(zmn∣θm)p(wmn∣zmn,φ)=∏k=1Kp(ϕk∣β)p(θm∣α)∏n=1Nmp(zmn∣θm)p(wmn∣zmn,φ) \begin{align} \tag{20.16} & p (\bs w_m, \bs z_m, \theta_m, \varphi | \alpha, \beta) \\ \notag = & \prod_{k = 1}^{K} p (\phi_k | \beta) p (\theta_m | \alpha) \prod_{\textcolor{red}{m} = 1}^{N_m} p (z_{mn} | \theta_m) p (w_{mn} | z_{mn}, \varphi) \\ \notag = & \prod_{k = 1}^{K} p (\phi_k | \beta) p (\theta_m | \alpha) \prod_{\textcolor{green}{n} = 1}^{N_m} p (z_{mn} | \theta_m) p (w_{mn} | z_{mn}, \varphi) \end{align} p(wm,∣θm,φ)=∏n=1K∫p(φk∣β)=∏k=1K∫p(φk∣β) \begin{align} \tag{20.18} p (\bs w_m, | \theta_m, \varphi) & = \prod_{\textcolor{red}{n} = 1}^{K} \int p (\varphi_k | \beta) \\ \notag & = \prod_{\textcolor{green}{k} = 1}^{K} \int p (\varphi_k | \beta) \end{align} p(w∣z,β)=∫p(w∣z,β)p(φ∣β)dφ=∫p(w∣z,φ)p(φ∣β)dφ \begin{align} \tag{20.23} p (w | z, \beta) & = \int p (w | z, \textcolor{red}{\beta}) p (\varphi | \beta) d \varphi \\ \notag & = \int p (w | z, \textcolor{green}{\varphi}) p (\varphi | \beta) d \varphi \\ \end{align} p(zi∣z−i,w,α,β)∝nkv+βv∑v−1V(nkv+βv)⋅nmk+αk∑k=1K(nmk+αk)∝nkv+βv∑v=1V(nkv+βv)⋅nmk+αk∑k=1K(nmk+αk) \begin{align} \tag{20.27} & p (z_i | \text{z}_{-i}, w, \alpha, \beta) \\ \notag \propto & \frac{n_{kv} + \beta_v}{\sum_{v \textcolor{red}{-} 1}^{V} (n_{kv} + \beta_v)} \cdot \frac{n_{mk} + \alpha_k}{\sum_{k = 1}^{K} (n_{mk} + \alpha_k)} \\ \notag \propto & \frac{n_{kv} + \beta_v}{\sum_{v \textcolor{green}{=} 1}^{V} (n_{kv} + \beta_v)} \cdot \frac{n_{mk} + \alpha_k}{\sum_{k = 1}^{K} (n_{mk} + \alpha_k)} \\ \end{align}