☰

圓州率
🌐
☰

Feature Image

機率論建構

數學, 機率論
引入機率論會使用到的集合論、極限、sigma-Field 的基本概念，並用測度論的方始討論機率測度。

引言

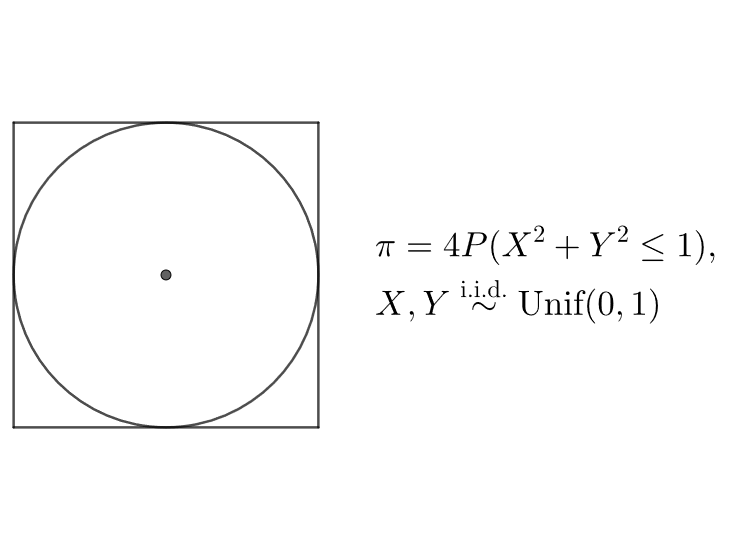
封面故事是用機率的方式計算出圓周率 π\pi，重複 nn 次獨立取出兩個介在 (0,1)(0, 1) 的數 XX 與 YY，定義 mm 是 X2+Y2≤1X^2 + Y^2 \leq 1 成立的次數，會發現隨著 nn 上升，4m/n4m / n 會逐漸往 π\pi 收斂，這就是靠採樣逼近圓周率的方式。

由 Laplace 首次定義機率為"目標事件數 / 總事件數"，然而這隱藏了每個事件都是同等機率 (equally likely)，且僅適用於有限 (finite) 事件，其適用性太低，因此我們會透過測度論的方式建構整個機率體系。

機率空間 (Probability Space)

定義 Ω\Omega 是蒐集所有可能樣本的集合，稱為樣本空間 (sample space)，任意 x∈Ωx \in \Omega 稱為樣本 (space)。F\mathcal F 是蒐集 Ω\Omega 子集合的集合，稱為事件空間 (event space)，任意 E∈FE \in \mathcal F 稱為事件 (event)。而評估事件發生機率的函數 P:F→[0,1]P : \mathcal F \to [0, 1]，稱其為機率函數 (probability function)。本段的目標在於建構出一個合理的 (Ω,F,P)(\Omega, \mathcal F, P) 稱為 機率空間 (probability space)。

例如骰子，其樣本空間就是

Ω={1,2,3,4,5,6} \Omega = \{1, 2, 3, 4, 5, 6\}

若我們關注的是"點數是奇數或偶數"的事件，則可以定義

F={{1,3,5},{2,4,6}} \mathcal F = \{ \{ 1, 3, 5 \}, \{ 2, 4, 6 \} \}

假設這顆骰子是公正的，則擲出偶數與奇數的事件理應相同，寫作

0.5=P({1,3,5})=P({2,4,6}) 0.5 = P (\{ 1, 3, 5 \}) = P (\{ 2, 4, 6 \} )

因此可以稱 (Ω,F,P\Omega, \mathcal F, P) 為"骰子點數是奇數或偶數"的機率空間。根據這個例子會發現，Ω\Omega 是自然產生的，F\mathcal F 是針對問題建構的，PP 也可能因為是非公正骰子而有所改動，因此我們需要定義 F\mathcal F 和 PP 的建構規則。

Sigma-Field

建構事件空間 F\mathcal F 時，我們需要確保其在集合操作下的封閉性 (closure)。F\mathcal F 被稱為 σ\sigma-field (sigma-field)，如果其滿足

  1. Ω∈F\Omega \in \mathcal F
  2. 若 E∈FE \in \mathcal F，則 Ec∈FE^c \in \mathcal F
  3. 若 E1,E2,⋯∈F\contiai{E} \in \mathcal F，則 ⋃i=1∞Ei∈F\bigcup_{i = 1}^{\infty} E_i \in F

根據 De Morgan's laws，若 F\mathcal F 是 σ\sigma-field 且 E1,E2,⋯∈F\contiai{E} \in \mathcal F 則 ⋂i=1∞Ei∈F\bigcap_{i = 1}^{\infty} E_i \in F。且 ∅\emptyset 與 Ω\Omega 存在於所有 σ\sigma-field。

Partition Construction

給定一個可數 Ω\Omega，從 Ω\Omega 的切分 (partition) 開始建構一個 σ\sigma-field，定義 ε={E1,E2,⋯}\varepsilon = \{ \contiai{E} \} 是 Ω\Omega 的 partition 滿足

  1. 互不相交 (pairwise disjoint): Ei∩Ej=∅E_i \cap E_j = \emptyset 對任意 i≠ji \ne j
  2. 且 ⋃i=1∞Ei=Ω\bigcup_{i = 1}^{\infty} E_i = \Omega

則可以寫作 F\mathcal F gnerated from ε\varepsilon

F=σ(ε)=P(ε)={S:S⊆ε} \mathcal F = \sigma (\varepsilon) = \mathcal P (\varepsilon) = \{ S : S \subseteq \varepsilon \}

其中 P(ε)\mathcal P (\varepsilon) 是指 ε\varepsilon 的 power set。

例如 Ω={1,2,3}\Omega = \{ 1, 2, 3 \}，令 ε1={{1},{2},{3}}\varepsilon_1 = \{ \{ 1 \}, \{ 2 \} , \{ 3 \} \} 和 ε2={{1,2},{3}}\varepsilon_2 = \{ \{ 1, 2 \}, \{ 3 \} \}，則

F1=σ(ε1)={∅,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}},F2=σ(ε2)={∅,{1,2},{3},{1,2,3}} \begin{align*} \mathcal F_1 & = \sigma (\varepsilon_1) = \{ \emptyset, \{ 1 \}, \{ 2 \} , \{ 3 \}, \{ 1, 2 \}, \{ 1, 3 \} , \{ 2, 3 \}, \{ 1, 2, 3 \} \}, \newline \mathcal F_2 & = \sigma (\varepsilon_2) = \{ \emptyset, \{ 1, 2 \}, \{ 3 \}, \{ 1, 2, 3 \} \} \end{align*}

對於有限 ∣ε∣=n|\varepsilon| = n，其建構的 σ\sigma-field 元素數量會是 2n2^n。

Borel Sigma-Field

此時若 Ω\Omega 是不可數，例 Ω=[0,1]\Omega = [0, 1]，以 F=σ({x}x∈Ω)\mathcal F = \sigma (\{ x \}_{x \in \Omega}) 建構方式雖然仍然是 σ\sigma-field，但不存在機率測度適用於此 F\mathcal F。

取而代之，會利用 Borel 建構方式，稱為 Borel σ\sigma-field

B=σ([x,y)x<y∈Ω) \mathcal B = \sigma ( [x, y)_{x < y \in \Omega} )

例如 [0,1][0, 1] 上的 Borel σ\sigma-field，{1}=[0,1)∈B\{1\} = [0, 1) \in \mathcal B，而任意 x∈[0,1)x \in [0, 1)，{x}=⋃i=1∞[x,x+1/i)∈B\{ x \} = \bigcup_{i = 1}^{\infty} [x, x + 1 / i) \in \mathcal B，因此 [0,1)∈B[0, 1) \in \mathcal B。而實數 R\bb R 上的 B\mathcal B 能透過上述相同方式證明 Q∈B\bb Q \in \mathcal B，根據封閉性得到 Qc∈B\bb Q^c \in \mathcal B，從而使 R∈B\bb R \in \mathcal B。

測度 (Measure)

接著要引入測度 (measure) 概念，目標是用個集合函數 (set function) μ\mu 來描述集合的大小。現給定 Ω\Omega 上的 σ\sigma-field F\mathcal F，稱一個集合函數 μ:F→R\mu : \mathcal F \to \bb R 是個測度 (measure)，若其滿足

  1. μ(E)≥0\mu (E) \geq 0 對任意 E∈FE \in \mathcal F
  2. μ(∅)=0\mu (\emptyset) = 0
  3. 可數可加性 (countalbe addivity): 對任意 {Ei:i∈N}⊂F\{ E_i : i \in \bb N \} \subset \mathcal F 且互不相交，則 μ(⋃i=1∞Ei)=∑i=1∞μ(Ei) \mu \left( \bigcup_{i = 1}^{\infty} E_i \right) = \sum_{i = 1}^{\infty} \mu (E_i)

稱 (Ω,F)(\Omega, \mathcal F) 為可測空間 (measurable space)，稱 F\mathcal F 為可測集 (measurable sets)，稱 (Ω,F,μ)(\Omega, \mathcal F, \mu) 為測度空間 (measure space)。

對應 Borel σ\sigma-field 的測度稱為 Lebesgue measure，定義為

L([x,y))=y−x L ([x, y)) = y - x

若 μ\mu 的輸出值都是有限的，即 μ(E)<∞\mu (E) < \infty 對任意 E∈FE \in \mathcal F，則稱 μ\mu 為 σ\sigma-finite measure。目標建構的機率空間就是測度空間的一個特例。

機率測度 (Probability Measure)

在可測空間 (Ω,F)(\Omega, \mathcal F) 上，機率測度 PP 是一種 σ\sigma-finite measure，其滿足

  1. P(Ω)=1P (\Omega) = 1
  2. P(A)∈[0,1]P (A) \in [0, 1]，對任意 A∈FA \in \mathcal F
  3. P(⋃i=1∞Ai)=∑i=1∞P(Ai)P (\bigcup_{i = 1}^{\infty} A_i) = \sum_{i = 1}^{\infty} P (A_i) 對任意互不相交 {Ai}i=1∞⊆F\{ A_i \}_{i = 1}^{\infty} \subseteq \mathcal F

其自然擁有的性質

  1. P(Ac)=1−P(A)P (A^c) = 1 - P (A)
  2. P(∅)=0P (\emptyset) = 0
  3. 若 A⊂BA \subset B，則 P(A)≤P(B)P (A) \leq P (B)
  4. P(A∪B)=P(A)+P(B)−P(AB)P (A \cup B) = P (A) + P (B) - P (AB)，其中 AB=A∩BAB = A \cap B
  5. Inclusion exclusion formula: P(A1∪⋯∪An)=∑i=1nP(Ai)−∑i1≤i2P(Ai1Ai2)+⋯+(−1)r+1∑i1≤⋯≤irP(Ai1⋯Air)+⋯+(−1)n+1P(A1⋯An) \begin{align*} P (A_1 \cup \cdots \cup A_n) & = \sum_{i = 1}^{n} P (A_i) - \sum_{i_1 \leq i_2} P (A_{i_1} A_{i_2}) + \cdots \newline & \quad + (-1)^{r + 1} \sum_{i_1 \leq \cdots \leq i_r} P (A_{i_1} \cdots A_{i_r}) + \cdots \newline & \quad + (-1)^{n + 1} P (A_1 \cdots A_n) \end{align*}

機率連續性

本段的目標在討論，給定事件序列 {En}n=1∞\{ E_n \}_{n = 1}^{\infty} ，在滿足何種條件下 PP 與 lim⁡\lim 具有交換性，即討論

lim⁡n→∞P(En)=?P(lim⁡n→∞En) \lim_{n \to \infty} P (E_n) \overset{?}{=} P \left( \lim_{n \to \infty} E_n \right)

其中需先定義集合序列 {En}n=1∞\{ E_n \}_{n = 1}^{\infty} 的極限

lim inf⁡n→∞En=⋃n=1∞⋂i=n∞Eiandlim sup⁡n→∞En=⋂n=1∞⋃i=n∞Ei \begin{align*} \liminf_{n \to \infty} E_n = \bigcup_{n = 1}^{\infty} \bigcap_{i = n}^{\infty} E_i \quad \text{and} \quad \limsup_{n \to \infty} E_n = \bigcap_{n = 1}^{\infty} \bigcup_{i = n}^{\infty} E_i \end{align*}

若 lim inf⁡nEn=lim sup⁡nEn\liminf_{n} E_n = \limsup_{n} E_n ，則定義 lim⁡nEn\lim_n E_n 存在且

lim⁡nEn=lim inf⁡nEn=lim sup⁡nEn \lim_n E_n = \liminf_{n} E_n = \limsup_{n} E_n

其擁有性質是

  1. lim inf⁡nEn⊆lim sup⁡nEn\liminf_{n} E_n \subseteq \limsup_{n} E_n

    證明lim inf⁡nEn=⋃n=1∞⋂i=n∞Ei=(⋂i=1∞Ei)∩(⋃n=2∞⋂i=n∞Ei)⊆⋂i=1∞Ei=⋂n=1∞En=⋂n=1∞⋃i=nnEi⊆⋂n=1∞⋃i=n∞Ei=lim sup⁡nEn \begin{align*} \liminf_{n} E_n & = \bigcup_{n = 1}^{\infty} \bigcap_{i = n}^{\infty} E_i \newline & = \left( \bigcap_{i = 1}^{\infty} E_i \right) \cap \left( \bigcup_{n = 2}^{\infty} \bigcap_{i = n}^{\infty} E_i \right) \newline & \subseteq \bigcap_{i = 1}^{\infty} E_i = \bigcap_{n = 1}^{\infty} E_n \newline & = \bigcap_{n = 1}^{\infty} \bigcup_{i = n}^{n} E_i \newline & \subseteq \bigcap_{n = 1}^{\infty} \bigcup_{i = n}^{\infty} E_i \newline & = \limsup_{n} E_n \end{align*}

  2. (lim inf⁡nEn)c=lim sup⁡nEnc(\liminf_{n} E_n)^c = \limsup_{n} E_n^c

    證明(lim inf⁡nEn)c=(⋃n=1∞⋂i=n∞Ei)c=⋂n=1∞(⋂i=n∞Ei)c=⋂n=1∞⋃i=n∞Eic=lim sup⁡nEnc \begin{align*} (\liminf_{n} E_n)^c & = \left( \bigcup_{n = 1}^{\infty} \bigcap_{i = n}^{\infty} E_i \right)^c \newline & = \bigcap_{n = 1}^{\infty} \left( \bigcap_{i = n}^{\infty} E_i \right)^c \newline & = \bigcap_{n = 1}^{\infty} \bigcup_{i = n}^{\infty} E_i^c \newline \newline & = \limsup_{n} E_n^c \end{align*}

  3. 若 {En}\{ E_n \} 是遞增的 (En⊆En+1E_n \subseteq E_{n + 1})，則 lim⁡nEn=⋃n=1∞En\lim_{n} E_n = \bigcup_{n = 1}^{\infty} E_n

    證明

    因為 {En}\{ E_n \} 是遞增的，所以 ⋂i=n∞Ei=En\bigcap_{i = n}^{\infty} E_i = E_n

    lim inf⁡n→∞En=⋃n=1∞⋂i=n∞Ei=⋃n=1∞Ei \liminf_{n \to \infty} E_n = \bigcup_{n = 1}^{\infty} \bigcap_{i = n}^{\infty} E_i = \bigcup_{n = 1}^{\infty} E_i

    另一邊，⋃i=n∞Ei=⋃i=1∞Ei\bigcup_{i = n}^{\infty} E_i = \bigcup_{i = 1}^{\infty} E_i 所以

    lim sup⁡n→∞En=⋂n=1∞⋃i=n∞Ei=⋂n=1∞⋃i=1∞Ei=⋃i=1∞Ei \limsup_{n \to \infty} E_n = \bigcap_{n = 1}^{\infty} \bigcup_{i = n}^{\infty} E_i = \bigcap_{n = 1}^{\infty} \bigcup_{i = 1}^{\infty} E_i = \bigcup_{i = 1}^{\infty} E_i

    因此

    lim⁡n→∞En=lim inf⁡n→∞En=lim sup⁡n→∞En=⋃i=1∞Ei \lim_{n \to \infty} E_n = \liminf_{n \to \infty} E_n = \limsup_{n \to \infty} E_n = \bigcup_{i = 1}^{\infty} E_i

  4. 若 {En}\{ E_n \} 是遞減的 (En⊇En+1E_n \supseteq E_{n + 1})，則 lim⁡nEn=⋂n=1∞En\lim_{n} E_n = \bigcap_{n = 1}^{\infty} E_n

最後推論出的性質是，若 lim⁡nEn=E\lim_{n} E_n = E，則機率測度 PP 與極限 lim⁡\lim 具有交換性，即

lim⁡n→∞P(En)=P(E)=P(lim⁡n→∞En) \lim_{n \to \infty} P (E_n) = P (E) = P \left( \lim_{n \to \infty} E_n \right)
證明

證明分兩步，第一步先證明當 EnE_n 是單調的 (monotone，即遞增或遞減的) 會滿足交換性，第二步再證明 lim⁡nEn=E\lim_{n} E_n = E 時滿足交換性。現假設 {En}\{E_n\} 是遞減的，則

lim⁡n→∞P(En)=lim⁡n→∞P(⋃i=1nEn)({En}遞減)=lim⁡n→∞P(⋃i=1nEn\En−1)(任意n,En\En−1互不相交)=lim⁡n→∞∑i=1nP(En\En−1)(σ-field定義3)=∑i=1∞P(En\En−1)=P(⋃i=1∞En\En−1)(σ-field定義3)=P(lim⁡n→∞En) \begin{align*} \lim_{n \to \infty} P (E_n) & = \lim_{n \to \infty} P \left( \bigcup_{i = 1}^{n} E_n \right) && (\{ E_n \} 遞減) \newline & = \lim_{n \to \infty} P \left( \bigcup_{i = 1}^{n} E_n \backslash E_{n - 1} \right) && (任意 n, E_n \backslash E_{n - 1} 互不相交) \newline & = \lim_{n \to \infty} \sum_{i = 1}^{n} P \left( E_n \backslash E_{n - 1} \right) && (\sigma\text{-field} 定義 3) \newline & = \sum_{i = 1}^{\infty} P \left( E_n \backslash E_{n - 1} \right) \newline & = P \left( \bigcup_{i = 1}^{\infty} E_n \backslash E_{n - 1} \right) && (\sigma\text{-field} 定義 3) \newline & = P \left( \lim_{n \to \infty} E_n \right) \end{align*}

若 {En}\{E_n\} 是遞增的，則 {Enc}\{E_n^c\} 會是遞減的，因此能套用上式

lim⁡n→∞P(En)=lim⁡n→∞1−P(Enc)=1−lim⁡n→∞P(Enc)=1−P(lim⁡n→∞Enc)=P[(lim⁡n→∞Enc)c]=P(lim⁡n→∞En) \begin{align*} \lim_{n \to \infty} P (E_n) & = \lim_{n \to \infty} 1 - P (E_n^c) \newline & = 1 - \lim_{n \to \infty} P (E_n^c) \newline & = 1 - P \left( \lim_{n \to \infty} E_n^c \right) \newline & = P \left[ \left( \lim_{n \to \infty} E_n^c \right)^c \right] \newline & = P \left( \lim_{n \to \infty} E_n \right) \end{align*}

最後，對於滿足 lim⁡nEn=E\lim_{n} E_n = E 的情況，定義 An=⋃i=n∞EiA_n = \bigcup_{i = n}^{\infty} E_i，則 {An}\{A_n\} 是遞減的且

P(lim⁡n→∞En)=P(lim sup⁡n→∞En)=P(⋂n=1∞⋃i=n∞En)=P(⋂n=1∞An)=lim⁡n→∞P(An) \begin{align*} P \left( \lim_{n \to \infty} E_n \right) & = P \left( \limsup_{n \to \infty} E_n \right) \newline & = P \left( \bigcap_{n = 1}^{\infty} \bigcup_{i = n}^{\infty} E_n \right) \newline & = P \left( \bigcap_{n = 1}^{\infty} A_n \right) \newline & = \lim_{n \to \infty} P (A_n) \end{align*}

相似的，定義 Bn=⋂i=n∞EiB_n = \bigcap_{i = n}^{\infty} E_i，則 {Bn}\{B_n\} 是遞減且

P(lim⁡n→∞En)=P(lim inf⁡n→∞En)=lim⁡n→∞P(Bn) \begin{align*} P \left( \lim_{n \to \infty} E_n \right) = P \left( \liminf_{n \to \infty} E_n \right) = \lim_{n \to \infty} P (B_n) \end{align*}

由於

Bn=⋂i=n∞Ei⊆En⊆⋃i=n∞Ei=An \begin{align*} B_n = \bigcap_{i = n}^{\infty} E_i \subseteq E_n \subseteq \bigcup_{i = n}^{\infty} E_i = A_n \end{align*}

因此

P(Bn)≤P(En)≤P(An) \begin{align*} P (B_n) \leq P (E_n) \leq P (A_n) \end{align*}

最後根據 lim⁡n→∞P(Bn)=lim⁡n→∞P(An)\lim_{n \to \infty} P (B_n) = \lim_{n \to \infty} P (A_n)，夾擠出

P(lim⁡n→∞En)=lim⁡n→∞P(En) \begin{align*} P \left( \lim_{n \to \infty} E_n \right) = \lim_{n \to \infty} P \left( E_n \right) \end{align*}

隨機變數 (Random Variable)

隨機變數 (random variable) XX 是從樣本空間映射至實數的函數，即 X:Ω→RX : \Omega \to \bb R。給定一個 σ\sigma-field F\mathcal F，稱 XX 是 F\mathcal F-measurable 的，若任意 Borel set B\mathcal B，

X−1(B)={ω∈Ω:X(ω)∈B}∈F \begin{align*} X^{-1} (\mathcal B) = \{ \omega \in \Omega : X (\omega) \in \mathcal B \} \in \mathcal F \end{align*}

要求 XX 是 F\mathcal F-measurable，是因為用數字 (R\bb R) 表達事件 (Ω\Omega)，並套用機率測度 P:F→RP : \mathcal F \to \bb R，因此要求 XX 是能被 F\mathcal F 刻劃的。

也經常用區間描述，例如

X−1((−∞,x])={X≤x}={ω∈Ω:X(ω)≤x}∈F \begin{align*} X^{-1} ((-\infty, x]) = \{ X \leq x \} = \{ \omega \in \Omega : X (\omega) \leq x \} \in \mathcal F \end{align*}

分布函數 (Distribution Function)

用函數 F:R→[0,1]F : \bb R \to [0, 1] 來描述隨機變數 XX 累積的機率分布，稱為 累積分布函數 (cumulative distribution function, cdf)

F(x)=P(X≤x) \begin{align*} F (x) = P (X \leq x) \end{align*}

然而以此定義的 FF 牽涉到隨機變數 XX (與背後的 σ\sigma-field F\mathcal F)，若僅給定一個函數 FF，稱其是個 cdf 若其滿足

  1. lim⁡x→−∞F(x)=0\lim_{x \to -\infty} F (x) = 0
  2. lim⁡x→∞F(x)=1\lim_{x \to \infty} F (x) = 1
  3. 單調 (monotonic increasing)：若 x1≤x2x_1 \leq x_2 則 F(x1)≤F(x2)F (x_1) \leq F (x_2)
  4. 右連續 (right continuous)：lim⁡x→c+F(x)=F(c)\lim_{x \to c^+} F (x) = F (c)

參考資料

  1. A Second Course in Probability, S. M. Ross, E. A. Pekoz