☰

圓州率
🌐
☰

Feature Image

Google PageRank

數學, 演算法
介紹 Google PageRank，Google 開發的搜尋結果的排序方案。

簡介

簡易範例

鄉村與都市的人口遷移問題，給定鄉村初始占總人口x(0)x^{(0)}的比例，都市則是y(0)y^{(0)}。鄉村有pp的遷出率，都市有qq的遷出率，則第tt年的人口狀態可以表達為

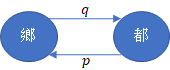
example

(x(t)y(t))=(1−pqp1−q)(x(t−1)y(t−1))=(1−pqp1−q)t(x(0)y(0)) \begin{align*} \left( \begin{array}{c} x^{(t)} \\ y^{(t)} \end{array} \right) & = \left( \begin{array}{cc} 1 - p & q \\ p & 1 - q \end{array} \right) \left( \begin{array}{c} x^{(t - 1)} \\ y^{(t - 1)} \end{array} \right) \\ & = \left( \begin{array}{cc} 1 - p & q \\ p & 1 - q \end{array} \right)^t \left( \begin{array}{c} x^{(0)} \\ y^{(0)} \end{array} \right) \end{align*}

若不考慮人口出生或死人，直覺上會覺得「無論起始值如何給定，只要時間夠長，最終一定會到收斂到平衡狀態。」即平衡狀態的存在性

(x∗y∗)(1−pqp1−q)=(x∗y∗) \begin{align*} \left( \begin{array}{c} x^* \\ y^* \end{array} \right) \left( \begin{array}{cc} 1 - p & q \\ p & 1 - q \end{array} \right) = \left( \begin{array}{c} x^* \\ y^* \end{array} \right) \end{align*}

與收斂性

lim⁡t→∞(x(t)y(t))=(x∗y∗) \begin{align*} \lim_{t \to \infty} \left( \begin{array}{c} x^{(t)} \\ y^{(t)} \end{array} \right) = \left( \begin{array}{c} x^* \\ y^* \end{array} \right) \end{align*}

現在將問題擴大成有NN座城市，初始的各城市人口占比為x(0)=(x1(0),x2(0),⋯ ,xN(0))T\bold{x}^{(0)} = (x_1^{(0)}, x_2^{(0)}, \cdots, x_N^{(0)})^T，並用一個N×NN \times N轉移矩陣 (stochastic matrix) MM表達遷移狀態，用MijM_{ij}表達從城市ii至城市jj的機率。則我們有

x(t)=Mx(t−1)=Mtx(0) \bold{x}^{(t)} = M \bold{x}^{(t - 1)} = M^t \bold{x}^{(0)}

設x∗\bold x^*為穩定狀態，則存在性問題即討論MM的 Eigenvector 是否存在，收斂性問題與起始點無關

x∗=Mx∗andlim⁡t→∞x(t)=x∗ \bold x^* = M \bold x^* \quad \text{and} \quad \lim_{t \to \infty} \bold x^{(t)} = \bold x^*

那最終我們可以把問題想像成

每個都市都是一個頁面，人口比例就是人們點進去這個網站的機率。

Google Pagerank

PageRank簡稱PR，是Google對搜尋結果排名的其中一個演算法。其假設為

重要的頁面會被更多其他頁面參照。

可應用於「圖論的有向性地圖權重」問題，藉由機率分布體現「某人在某個頁面的機率」。用PR(A)PR(A)表示「某人停在AA頁面的機率，亦表示為AA頁面在集合內的權重」。若PR(A)=0.3PR (A) = 0.3，則表示有0.3的機率出現在AA頁面。而所有的頁面PR值合為1。

簡化模型

假設

  1. 頁面不允許自我參照；
  2. 頁面至少參照一個頁面；

若參照情況如下

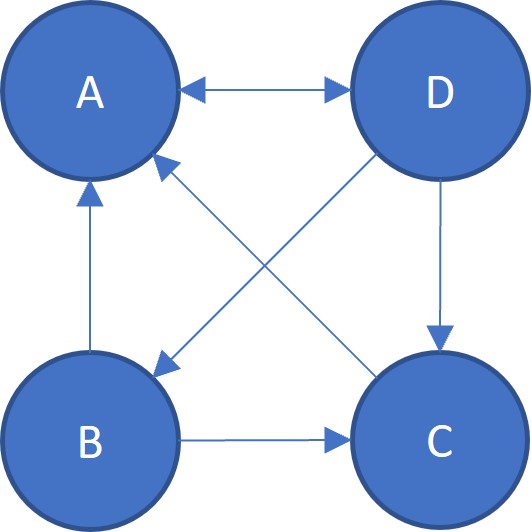
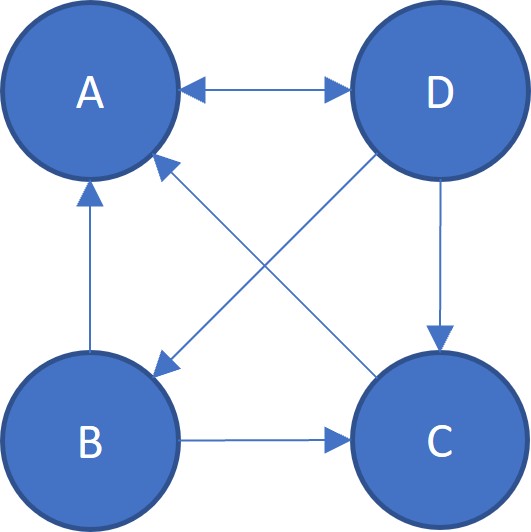
B頁面參照A與C頁面，即B給與A與C各1/21/2票。同理，也能看出D給與A、B與C各1/31/3票。故A獲得B的1/21/2票、C的1票、與D的1/31/3票。

PR(A)=PR(B)2+PR(C)1+PR(D)3 PR (A) = \frac{PR(B)}{2} + \frac{PR(C)}{1} + \frac{PR(D)}{3}

同理

PR(B)=PR(D)1 PR (B) = \frac{PR (D)}{1}

若有NN個頁面p1,p2,⋯ ,pNp_1, p_2, \cdots, p_N，設M(pi)M (p_i)為有參照pip_i頁面的集合，L(pj)L (p_j) 為pjp_j頁面所參照的頁面數量，則任意頁面pip_i可以寫為

PR(pi)=∑pj∈M(pi)PR(pj)L(pj) PR (p_i) = \sum_{p_j \in M (p_i)} \frac{PR (p_j)}{L (p_j)}

解非唯一

在簡化模型中，會出現PR值得解非唯一的情況，考慮以下參照狀態

M=(0100100000010010) M = \left( \begin{array}{cccc} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ \end{array} \right)

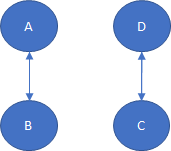
example_1

則顯然的

(0.250.250.250.25),(0.50.500),(000.50.5) \begin{align*} \left( \begin{array}{c} 0.25 \\ 0.25 \\ 0.25 \\ 0.25 \end{array} \right), \left( \begin{array}{c} 0.5 \\ 0.5 \\ 0 \\ 0 \end{array} \right), \left( \begin{array}{c} 0 \\ 0 \\ 0.5 \\ 0.5 \end{array} \right) \end{align*}

都能成為解，事實上

x=(0.50.500)t1+(000.50.5)t2 \begin{align*} \bold x = \left( \begin{array}{c} 0.5 \\ 0.5 \\ 0 \\ 0 \end{array} \right) t_1 + \left( \begin{array}{c} 0 \\ 0 \\ 0.5 \\ 0.5 \end{array} \right) t_2 \end{align*}

對任意 t1+t2=1t_1 + t_2 = 1 都能成為解。問題出在 nullity(M)≥1\text{nullity} (M) \geq 1，即 Eigenspace 太大使得 x\bold x 的解非唯一。

完整模型

上述我們做了2項假設，其中的第2假設「頁面至少參照一個頁面」，若某頁面不參照其他任何頁面，則會導致該頁面的PR值像個黑洞一樣只進不出。為防止這個情況，做出以下設定「若某頁面不參照其他頁面，則視為參照其他所有頁面。」

給定一個d∈(0,1)d \in (0, 1)，改變計算PR值的方式為

PR(pi)=1−dN+d∑pj∈M(pi)PR(pj)L(pj) PR (p_i) = \frac{1 - d}{N} + d \sum_{p_j \in M (p_i)} \frac{PR (p_j)}{L (p_j)}

這邊的dd為阻尼係數(damping factor)視為隨機瀏覽者(random surfer)根據推送到下一個頁面的機率，而1−d1 - d就視為隨機到任一個網站的機率。一般預設d=0.85d = 0.85，由一般上網者使用瀏覽器書籤功能的頻率的平均值估算得到。

原始論文版本

特別注意，PR值為機率值，我們假設

∑i=1NPR(pi)=1 \sum_{i = 1}^{N} PR (p_i) = 1

而在原始的版本中

PR(pi)=(1−d)+d∑pj∈M(pi)PR(pj)L(pj) PR (p_i) = (1 - d) + d \sum_{p_j \in M (p_i)} \frac{PR (p_j)}{L (p_j)}

會導致

∑i=1NPR(pi)=N≠1 \sum_{i = 1}^{N} PR (p_i) = N \ne 1

因此我們不採用原始版本

矩陣形式

設定一個鄰接函數(adjacency function)，由於我們假設網站不能自我參照，故任意頁面pi↛pip_i \not \to p_i

l(pi,pj)={1/L(pj)ifpj→pi0ifpj↛pi l (p_i, p_j) = \left\lbrace \begin{array}{lll} 1 / L (p_j) & \text{if} & p_j \to p_i \\ 0 & \text{if} & p_j \not \to p_i \end{array}\right.

使得

PR(pi)=1−dN+d⋅l(pi,pj)⋅PR(pj) PR (p_i) = \frac{1 - d}{N} + d \cdot l (p_i, p_j) \cdot PR (p_j)

因此用矩陣形式可以如下表達，設定x\bold x 為PR值組成的向量

x=(PR(p1)PR(p2)⋮PR(pN)) \bold x = \left( \begin{array}{c} PR (p_1) \\ PR (p_2) \\ \vdots \\ PR (p_N) \\ \end{array} \right)

MM是鄰接函數組成的矩陣Mij=l(pi,pj)M_{ij} = l (p_i, p_j)，

M=(l(p1,p1)l(p1,p2)⋯l(p1,pN)l(p2,p1)l(p2,p2)⋯l(p2,pN)⋮⋮⋮l(pN,p1)l(pN,p2)⋯l(pN,pN)) M = \left( \begin{array}{cccc} l (p_1, p_1) & l (p_1, p_2) & \cdots & l (p_1, p_N) \\ l (p_2, p_1) & l (p_2, p_2) & \cdots & l (p_2, p_N) \\ \vdots & \vdots & & \vdots \\ l (p_N, p_1) & l (p_N, p_2) & \cdots & l (p_N, p_N) \\ \end{array} \right)

使得RR能以簡潔的形式表達

x=1−dN1N+dMx \bold x = \frac{1 - d}{N} \textbf{1}_N + d M \bold x

其中的1N=(1 1 ⋯ 1)T∈RN\textbf{1}_N = (1 \ 1 \ \cdots \ 1)^T \in \mathbb R^N。

由於∑i=1nxi=1\sum_{i = 1}^{n} \bold x_i = 1，定義一個N×NN \times N矩陣Eij=1/NE_{ij} = 1 / N，則

Ex=1N1N E\bold x = \frac{1}{N} 1_N

故矩陣形式的x\bold x 可以改寫成

x=1−dN1N+dMx=[(1−d)E+dM]x \begin{align*} \bold x & = \frac{1 - d}{N} \textbf{1}_N + d M \bold x \\ & = \left[ (1 - d) E + d M \right] \bold x \end{align*}

定義M^=(1−d)E+dM\hat M = (1 - d) E + d M，其中Eij=1/NE_{ij} = 1 / N且Mij=l(pi,pj)M_{ij} = l (p_i, p_j)，則上述公式改寫

x=M^x \bold x = \hat M \bold x

唯一性與收斂性

參考至 The Second Eigenvalue of the Google Matrix

計算

Power Method

起始值 x(0)\bold x^{(0)} 將PR平均分配給 NN 個頁面，設 x(t)\bold x^{(t)} 為的第 tt 次迭代PR值，接著重複迭代去逼近穩定狀態

x(0)=1N1Nx(t+1)=M^x(t) \begin{align*} \bold x^{(0)} & = \frac{1}{N} \textbf{1}_N \\ \bold x^{(t + 1)} & = \hat M x^{(t)} \end{align*}

給定網站數量N=10N = 10，首先隨機生成網站的參照況狀。若R[i][j]是1表示pi→pjp_i \to p_j；反之若是0則表示pi↛pjp_i \not \to p_j。

N = 10 # Number of pages

import random
import numpy as np

R = np.zeros((N, N), dtype=int) # Reference state of pages
for i in range(N):
    for j in range(N):
        R[i][j] = 1 if random.random() < 0.3 else 0
    R[i][i] = 0
print(R)

python

隨機給出

[[0 0 1 0 1 0 0 0 1 0]
 [1 0 0 1 0 0 0 0 0 0]
 [1 0 0 0 0 0 1 0 0 1]
 [0 0 1 0 1 1 0 0 0 1]
 [0 1 1 0 0 0 0 1 1 0]
 [1 0 0 0 0 0 1 0 0 1]
 [0 0 1 0 0 1 0 0 0 0]
 [1 0 0 0 1 0 0 0 0 0]
 [0 0 0 1 0 1 0 0 0 1]
 [0 0 0 0 1 0 1 0 1 0]]

python

根據L(pi)L (p_i)的定義為pip_i頁面參照的總數，故L(pi)L (p_i)等於R的列和，用L矩陣儲存L(p1)L (p_1)、L(p2)L (p_2)、⋯\cdots、L(pN)L (p_N)。給定d=0.85d = 0.85並依此生成出M^\hat M

d = 0.85
N = R.shape[1] # Number of pages
L = np.array([sum(R[i]) for i in range(N)]) # Adjacency function
M = np.zeros((N, N)) 
for i in range(N):
    if L[i] != 0:
        for j in range(N):
            M[j][i] = R[i][j] / L[i]
    else:
        for j in range(N):
            M[j][i] = 1 / N
M_hat = d * M + (1 - d) / N
print(M_hat)

python

計算出M^\hat M

[[0.015      0.44       0.29833333 0.015      0.015      0.29833333
  0.015      0.44       0.015      0.015     ]
 [0.015      0.015      0.015      0.015      0.2275     0.015
  0.015      0.015      0.015      0.015     ]
 [0.29833333 0.015      0.015      0.2275     0.2275     0.015
  0.44       0.015      0.015      0.015     ]
 [0.015      0.44       0.015      0.015      0.015      0.015
  0.015      0.015      0.29833333 0.015     ]
 [0.29833333 0.015      0.015      0.2275     0.015      0.015
  0.015      0.44       0.015      0.29833333]
 [0.015      0.015      0.015      0.2275     0.015      0.015
  0.44       0.015      0.29833333 0.015     ]
 [0.015      0.015      0.29833333 0.015      0.015      0.29833333
  0.015      0.015      0.015      0.29833333]
 [0.015      0.015      0.015      0.015      0.2275     0.015
  0.015      0.015      0.015      0.015     ]
 [0.29833333 0.015      0.015      0.015      0.2275     0.015
  0.015      0.015      0.015      0.29833333]
 [0.015      0.015      0.29833333 0.2275     0.015      0.29833333
  0.015      0.015      0.29833333 0.015     ]]

python

給定最大迭代次數T = 100，並用record_x記錄每次x迭代的結果。

T = 100
x = np.ones(N) / N
record_x = [x]

for t in range(T):
    x = M_hat @ x
    record_x.append(x)

print(record_x[-1])

python

計算x(100)\bold x^{(100)}是

[0.12047504 0.03982829 0.14011    0.0634499  0.11683903 0.11266998
 0.1239153  0.03982829 0.1112572  0.13162697]

python

完整個PR函式為

N = 10 # Number of pages

import random
import numpy as np

R = np.zeros((N, N), dtype=int) # Reference state of pages
for i in range(N):
    for j in range(N):
        R[i][j] = 1 if random.random() < 0.3 else 0
    R[i][i] = 0

def PR(R: np.ndarray, T = 32, d = 0.85):
    '''
    R: Reference matirx
    T: Number of iterations
    d: Camping factor
    '''
    N = R.shape[1] # Number of pages
    L = np.array([sum(R[i]) for i in range(N)]) # adjacency function
    M = np.zeros((N, N)) 
    for i in range(N):
        if L[i] != 0:
            for j in range(N):
                M[j][i] = R[i][j] / L[i]
        else:
            for j in range(N):
                M[j][i] = 1 / N
    M_hat = d * M + (1 - d) / N

    x = np.ones(N) / N
    for i in range(T):
        x = M_hat @ x
    
    return x

print(PR(R))

python

結果分析

若迭代的次數足夠多，x(t)\bold x^{(t)}的變化量應趨近於00，即

f(t)=∥x(t)−x(t−1)∥2→0 f (t) = \| \bold x^{(t)} - \bold x^{(t - 1)} \|_2 \to 0

並觀察x(t)\bold x^{(t)}的收斂速度

g(t)=f(t−1)/f(t) g (t) = f (t - 1) / f (t) 
from numpy import linalg as LA
import matplotlib.pyplot as plt
import math

f = [LA.norm(record_x[t] - record_x[t - 1]) for t in range(1, T)]
log_f = [math.log(f[i]) for i in range(1, T - 1)]
g = [f[t - 1] / f[t] for t in range(1, T - 1)]

plt.figure(0)
plt.xlabel('t')
plt.ylabel('f (t)')
plt.plot(f)

plt.figure(1)
plt.xlabel('t')
plt.ylabel('ln f(t)')
plt.plot(log_f)

plt.figure(2)
plt.xlabel('t')
plt.ylabel('g (t)')
plt.plot(g)

python

發現f(t)f (t)隨著tt上升而遞減

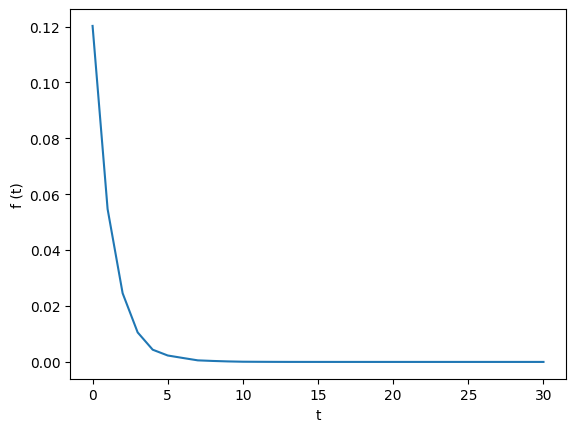
analysis_1

且ln⁡f(t)\ln f (t)與tt的關係大約呈現線性

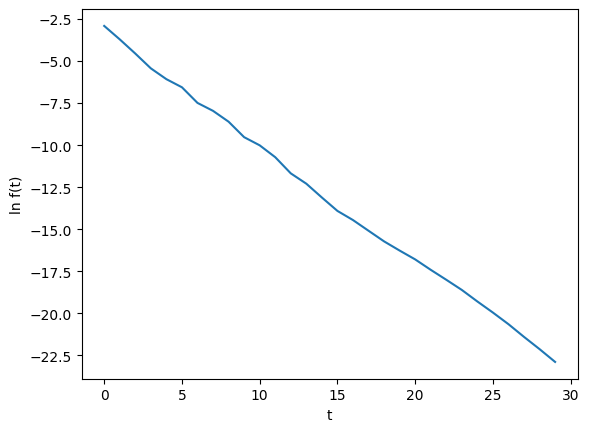
analysis_2

ln⁡f(t+30)−ln⁡f(t)≈−20 \ln f (t + 30) - \ln f (t) \approx - 20

假設log⁡f(t)\log f (t)滿足線性關係使得，則可解出a=−23a = - \frac{2}{3}與b=−52b = - \frac{5}{2}，即

f(t)≈10−23t−52 f (t) \approx 10^{- \frac{2}{3} t - \frac{5}{2}}

而g(t)g (t)則在2左右波動，滿足前面的假設

g(t)=f(t−1)f(t)≈e2/3≈1.95 g (t) = \frac{f (t - 1)}{f (t)} \approx e^{2/3} \approx 1.95

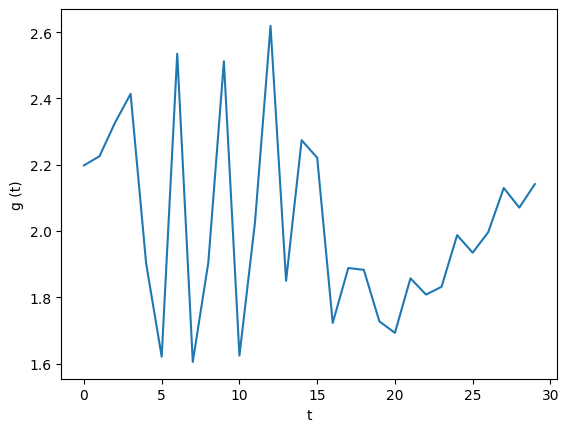
analysis_3

觀察多次實驗，在N=10、N = 10、 d=0.85d = 0.85與「0.3的隨機參照機率」的條件下多次嘗試

  1. PR值的誤差逐漸縮小，即f(t)→0f (t) \to 0
  2. PR值得誤差量每次約少2倍，即g(t)≈2g (t) \approx 2

特別注意，在最開始生成C矩陣的時候，任意頁面參照其他頁面的機率設為0.3，即

Prob(Pi→Pj)=0.3,i≠j Prob (P_i \to P_j) = 0.3, \quad i \ne j

我認為收斂速度會被下列因素影響

  1. 頁面數量NN，數量越多收斂越慢
  2. 阻尼係數dd，不確定影響關係
  3. 隨機參照機率，不確定影響關係

附件

原始文獻

  1. BRIN, Sergey; PAGE, Lawrence. The anatomy of a large-scale hypertextual web search engine. Computer networks and ISDN systems, 1998, 30.1-7: 107-117.

Google 的資料

Google搜尋引擎的資料庫收錄超過千億網頁，檔案大小超過100,000,000 GB。

https://www.google.com/search/howsearchworks/how-search-works/organizing-information/

新算法

根據Google前員工的說法，”PageRank自2006年以來就沒有被使用過”，取而代之的新算法是

https://patents.google.com/patent/US9165040B1/en