客戶個性建模與評估

本研究將對客戶個性進行建模，處理財務資料中常見的高共線性與異常值問題，引入穩健性羅吉斯回歸分析，預測客戶是否會參與活動。根據預測目標資料的不平衡，放棄了常用的準確率指標，開發基於利潤的模型評估指標，以達到利潤最大化做為模型選擇。最後根據變數的主成分選擇，並分析與探討該項活動背後市場的定位以及找出潛在客戶的特徵。

2024/06/12 最後更新: 2025/01/25

引言

本研究我負責建構客戶參與度的機器學習模型，與財經專業的侯威志合作，他提供財經角度資料分析與模型解釋。

下載客戶個性建模與評估.pdf。

下載英文版 Customer Personality Modeling and Evaluation.pdf。

摘要

關鍵字：客戶個性分析、機器學習、穩健性。

簡介

客戶個性建模能協助企業挖掘潛在客戶以增加收益，並執行精準行銷以減少支出。在活動推廣與產品行銷上，並非所有客戶均會參與，執行精準行銷能有效減少行銷支出；透過客戶特徵預測，能協助企業辨識潛在客戶。本研究資源自 kaggle，資料包含 2000 位客戶資料與 19 種客戶特徵，目標是基於客戶特徵預測是否參與行銷活動，而本資料具有以下數個屬性：

多個變數具有異常值，例：年齡。
多個變數具有高度共線性，例：年齡、收入、家中孩童數量。
預測目標極度不平衡，活動僅有7%的參與者。
基於資料匿名性，行銷活動的主題是未知的。

由於存在大量異常值，傳統線性模型會產生嚴重偏差，本研究引入穩健性(robust)建模；利用主成分分析(principal component analysis, PCA)消除共線性，建立數個簡易指標；使用羅吉斯迴歸(logistic regression, LR)建構出具有強解釋力模型；最後由於預測目標的不平衡，捨棄常用的精確度，開發出基於毛利(profit)的評估指標。以此向企業回答活動可能收益、鎖定潛在客群、協助企業建立精準行銷策略。

建模

基於資料具有強共線性且需要解釋性模型的目標，因此先執行主成份分析 (principal component analysis, PCA)，並選用羅吉斯迴歸 (logistic regression, LR) 進行建模；由於資料的多個維度有大量異常值，傳統的線性建模會產生嚴重的估計誤差，因此需要穩健性估計量，用以降低異常值影響，引入穩健性 PCA (robust PCA, RPCA) 與穩健性 LR (robust LR, RLR)；模型實做選用 R 語言的 rrcov 包中的 PcaHubert 執行 RPCA，與 robustbase 包中的 glmrob 執行 RLR。

穩健性主成份分析

設原始資料矩陣為 $M \in \mathbb R^{n \times p}$ ，PCA 會將資料點投影到超平面上，令 $x_i \in \mathbb R^p$ 為第 $i$ 筆資料的座標， $p_{x_i}$ 為投影後的第 $i$ 筆資料的座標，PCA 的最小化目標為原始資料點與投影點的距離差，即

\begin{align*} \| M \|_* = \min \sum_{i = 1}^{n} \| x_i - p_{x_i} \|^2 \end{align*}

而 PCA 容易受到異常值影響，因此 RPCA 假設多數資料具有高共線性資料 $L$ ，並存在少量的異常值 $S$ ，使得 $M = L + S$ ，將最小化目標改為：

\begin{align*} \min_{L + S = M} \| L \|_* + \lambda \| S \|_1 \end{align*}

其中 $\| S \|_1 = \sum_{ij} |S_{ij}|$ ， $\lambda > 0$ 是調整變數，決定異常點影響力， $\lambda$ 越小則會傾向將更多資料視為異常值，若將後項 $\|S\|_1$ 移除後將退化成 PCA。

公式 (2) 中，若是能辨識出異常值，並將其視為 $S$ 中的點，將能使多數資料 $L$ 的 PCA 投影更加適配，大幅減少 $\|L\|_*$ 數值；然而 $\|S\|_1$ 的成長速度相較於 $\|L\|_*$ 更快，僅能將少量的點移動至 $S$ 作為平衡。

穩健性羅吉斯迴歸

預測目標的活度參與狀況設為 $y$ ，若第 $i$ 位客戶參與活動，則 $y_i = 1$ ，反之則為 $y_i = 0$ 。LR 透過 sigmoid 函數 ( $\sigma$ ) 將資料的線性組合轉換至 $(0, 1)$ 區間內，預測客戶是否參與活動的指標為

\begin{align*} \hat y = \sigma (x^T \beta) = \frac{\exp (x^T \beta)}{1 + \exp (x^T \beta)} \end{align*}

其中 $\beta$ 的選擇取決於最小化目標 Cross-Entropy Loss：

\begin{align*} \varepsilon_i & = \begin{cases} - \ln (\hat y_i) & \text{if } y_i = 1 \\ - \ln (1 - \hat y_i) & \text{if } y_i = 0 \\ \end{cases} \\ & = - y_i \ln (\hat y_i) - (1 - y_i) \ln (1 - \hat y_i) \end{align*}

LR 作為廣義線性模型，也容易受到異常值影響，而穩健性常用的大致有三種：

權重殘差：轉換原始殘差，例如對每筆資料的權重設定為其殘差的倒數，並重新迭代數次；或者是透過常態分佈的密度函數 $\begin{align*} f (\varepsilon) = \frac{1}{\sqrt{2 \pi}} \exp \left( - \frac{\varepsilon^2}{2} \right) \end{align*}$ 使得殘差越小權重越大。
穩健性損失函數：設定損失函數的上限，例如設定門檻值 $t$ ，將超過門檻的殘差降低至 $t$ ，如： $\begin{align*} f (\varepsilon) & = \begin{cases} \varepsilon & \text{if } \varepsilon \leq t \\ t & \text{if } \varepsilon > t \\ \end{cases} \\ & = \varepsilon I \{ \varepsilon \leq t \} + t I (\varepsilon > t) \end{align*}$
隨機採樣共識 (random sample consensus)：概念與 RPCA 類似，其目標在於識別異常值，透過隨機採樣發現某些點在訓練集模型時，測試精確度可能會嚴重下降，並以此作為是否為異常值參考標準，並考慮降低異常值權重或是移除後重新建模。

模型評估

透過 RLR 後，對每位客戶產生介於 $(0, 1)$ 的預測值 $\hat y$ ，數值越大則認為越有可能參與活動，此時須選擇一個門檻值 $t$ ，以 $\tilde y = I \{ \hat y > t \}$ 作為決定預測的類別，然而依據資料不平衡的特性，設定 $t = 1$ 會使所有預測值都為 0，因而獲得 93% 的精確度，但這並非一個合理的選擇，也因此 $t$ 的選擇以最大化精確度並非合理的選項。

受到 ROC 啟發，本研究以毛利作為評估標準

\begin{align*} \text{Profit}_{t, g} = \text{TP}_t (g - 1) - \text{FP}_t \end{align*}

其中 g 的定義為獲利比率，也就是我們賣出一單位商品會有 g% 的獲利；而TP (true positive) 與 FP (false positive) 均會受到 $t$ 的選擇影響

\begin{align*} \text{TP}_t & = \sum_{i = 1}^{n} I \{ y_i = 1, \tilde y_i = 1\} = \sum_{i = 1}^{n} I \{ y_i = 1 \} I \{ \hat y_i > t \} \\ \text{FP}_t & = \sum_{i = 1}^{n} I \{ y_i = 0, \tilde y_i = 1\} = \sum_{i = 1}^{n} I \{ y_i = 0 \} I \{ \hat y_i > t \} \end{align*}

在給定 $g$ 的前提下，選擇

\begin{align*} t = \argmax_{t \in [0, 1]} \text{Profit}_{t, g} = \argmax_{t \in [0, 1]} [ \text{TP}_t (g - 1) - \text{FP}_t] \end{align*}

以此做為門檻值，若客戶預測 $\hat y_i$ 大於 $t$ 後則寄邀請信，並以 $\max_{t \in [0, 1]} \text{Profit}_{t, g}$ 回答此活動的潛在利潤，並在後續的研究確定 $g$ 的選擇並不會嚴重影響 $t$ 的選擇。

以執行過 RPCA 與 RLR 的模型為例，下圖左側是對 30% 測試資料集合的 ROC 曲線。給定 $g = 10$ ，透過毛利公式轉換，獲得右圖，此時選擇 $t$ 使得 FP 落在 0.2 左右時，能獲得最高毛利估計 230。

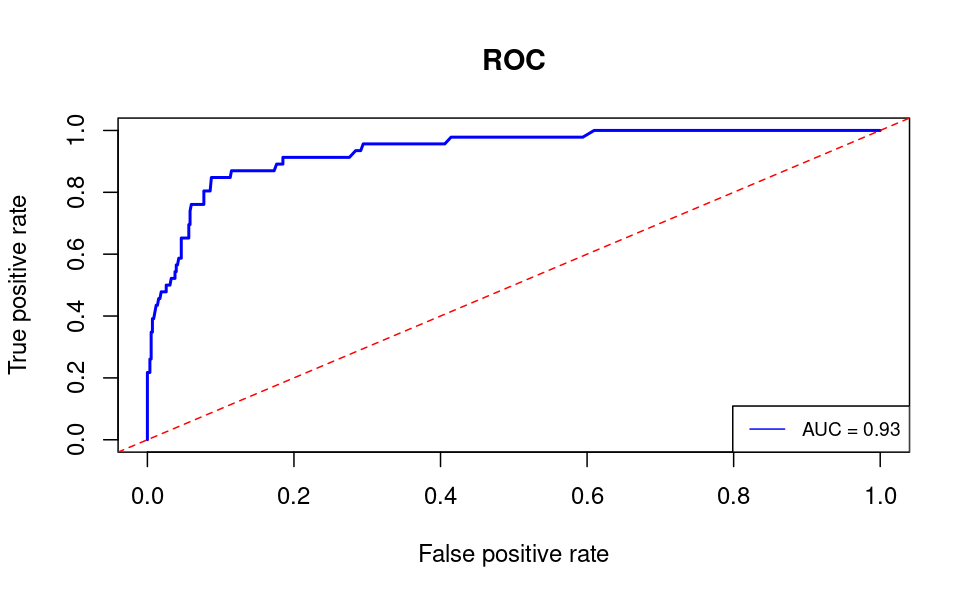
此時選取 $g$ 在 7 至 20 間，相對應的 $t$ 影響並不大，其對應 FP 均落在 0.2 附近，因此 $g$ 的選取可經由過往活動經驗或該市場上商品定位選取即可，在合理的獲利比率範圍內的選取並不會對預測結果產生重大變化。以毛利作為評估標準，本研究也比較出不同機器學習模型，如 linear discriminant analysis (LDA)、random forest (rf)、classification and regression tree (CART) 等模型之間的表現，觀察不同模型下針對 Profit 獲利能力選取最大獲利模型，能看出使用 RPCA 作為變數的RLR表現與其他機器模型差不多持平，於是我們挑選 RLR 此模型作往後探討。改變 $g$ 時的 $t$ 擇變動與不同模型之間的比較。

結論

面對多維度含有異常值的資料，線性模型的估計量具有嚴重偏差，而對每個維度逐一檢查的確可行，但並不具有效率，透過穩健性建模能在盡可能保留資料的前提下，有效排除異常值的影響。

以精確度做為評估模型的標準，這意謂不同類群的權重是相同的，也等價於不同類群的估計錯誤代價相同，然而在這筆資料中不同類群的代價顯然不同，將參與者預測成不參與者會導致利潤下降，而將不參與者預測成參與者僅是增加一點行銷支出。開發以利潤最大化的評估方式，不僅能平衡不同類群之間的錯誤代價，也能回答出活動潛在收入。

解析RLR結果，其中 4 項指標為 RPCA 結果

	Est	S.E.	Z-value	P-value
截距	-1.69	0.09	-17.92	2e-16
收入指標	0.75	0.03	22.29	2e-16
年輕族群指標	0.48	0.05	10.19	2e-16
消費頻率指標	0.24	0.05	4.53	5.81e-06
消費力指標	-0.50	0.05	-10.06	2e-16

解釋 RPCA 結果，以變數係數的絕對值大於 0.2 作為顯著性依據。

PC1，收入指標：有多少小孩在家為負相關，而消費偏好平台、葡萄酒銷售量、所得為正影響，因此將PC1建立一個收入指標，並根據收入為重要指標來看，廠商能參與價格的制定與買賣模式，因此推論此市場為獨占性競爭市場，再根據其表單的設計變數來看，我們認為此市場可能為有品牌的零售業或大賣場。
PC2，年輕族群指標：有多少青年人在家為負相關，而出生年份為正相關，因此將PC2建立一個年輕族群指標，我們推論此活動的可能主要客群應為年輕的會員，其較有意願參與此活動。
PC4，消費頻率指標：距離最近一次消費的天數為負指標，因此將 PC4 建立一個消費頻率指標，也能結合 PC1 反映此為大賣場的可能性提高，畢竟大賣場的消費頻率不會說太高，很少天天去消費，可能每周或每個月才會進行一次大採買。
PC6，消費力指標：葡萄酒銷售量為正相關，而一些民生食材上的消費、家裡有多少小孩及青年人為負指標，因此將 PC6 建立一個消費力指標，我們推論這些相關的占我們一個家庭主要支出的比例極高，且為必須品上的支出。

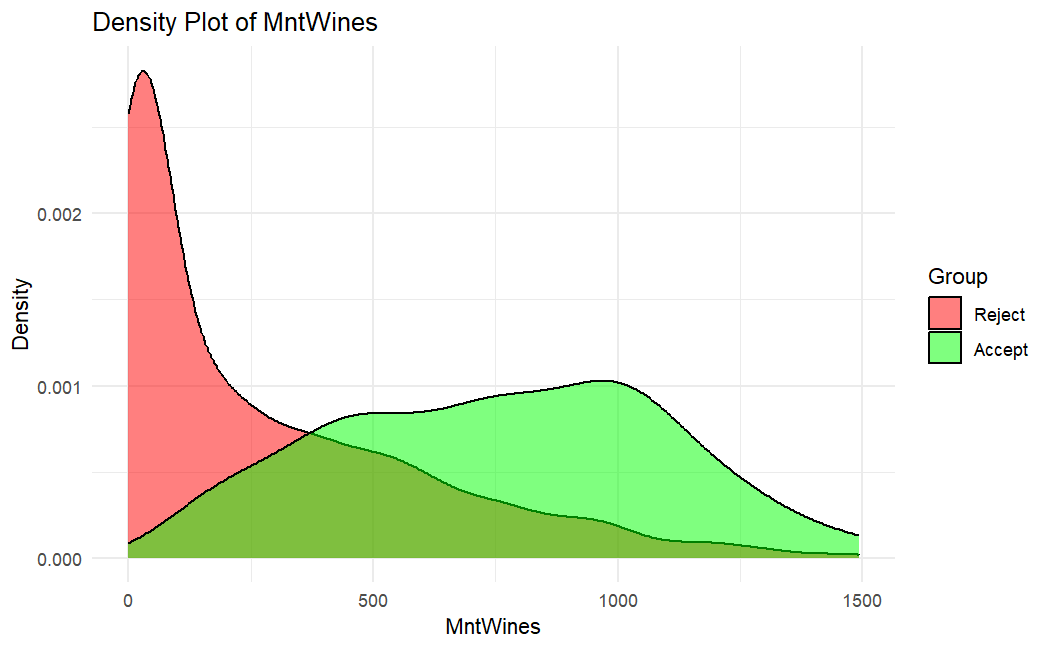
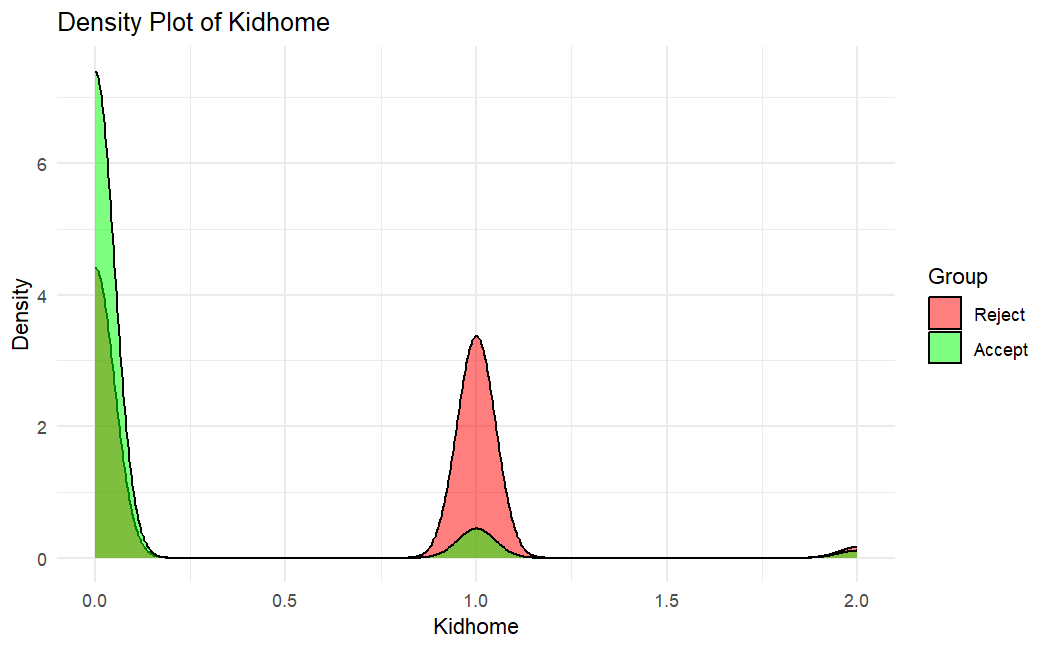
最後，基於上述推論市場的特質，與在家庭資源分配的研究，觀察是否參與活動的兩族群在酒類消費與家中孩童數量的密度分布。推論出此活動可能為大賣場在做葡萄酒的促銷活動，且有較高意願參與此活動的會是年輕族群，或是家中小孩愈少的家庭愈容易參與此活動的消費。

參考資料

Feng, J., Xu, H., Mannor, S. and Yan, S. (2014), Robust Logistic Regression and Classification, in 'Advances in Neural Information Processing Systems', Vol. 27, Curran Associates, Inc.
Hong, Y.-F. (2017), The Measurement of Child Costs and Interhousehold Resource Allocation—Evidence from Taiwan, 國立中央大學.
Hubert, M., Rousseeuw, P. J. and Vanden Branden, K. (2005), 'ROBPCA: A New Approach to Robust Principal Component Analysis', Technometrics 47(1), 64–79.