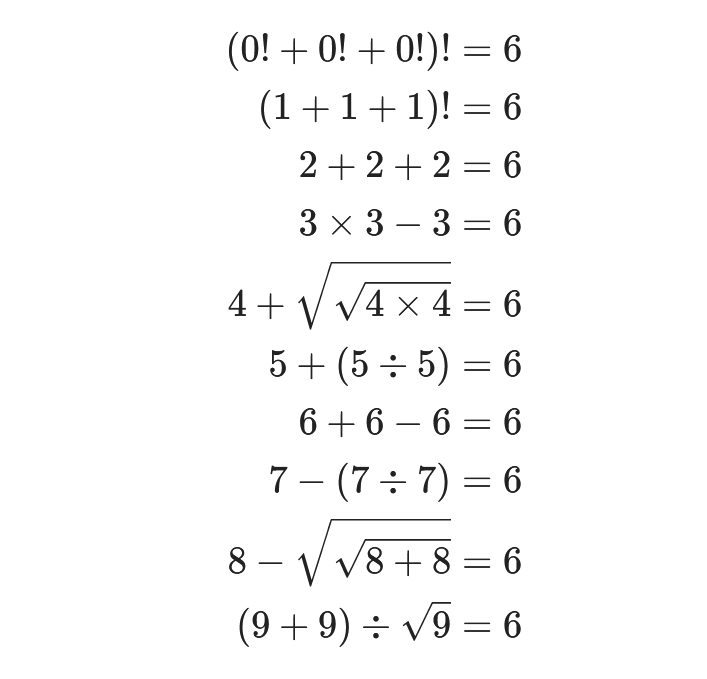變成 6
把數字湊成6。
加上一些符號,讓下列的式子成立
000=6111=6222=6333=6444=6555=6666=6777=6888=6999=6例如
2+2+2=63×3−3=6參考解答
(0!+0!+0!)!(1+1+1)!2+2+23×3−34+4×45+(5÷5)6+6−67−(7÷7)8−8+8(9+9)÷9=6=6=6=6=6=6=6=6=6=6這邊一共用了+, −, ×, ÷, !, (), 共7種操作,能不能只用到5種操作?
(0!+0!+0!)!(1+1+1)!(⌊2⌋+⌊2⌋+⌊2⌋)!(⌊3⌋+⌊3⌋+⌊3⌋)!(⌊4⌋+⌊4⌋+⌊4⌋)!(⌊5⌋+⌊5⌋+⌊5⌋)!(⌊6⌋+⌊6⌋+⌊6⌋)!(⌊7⌋+⌊7⌋+⌊7⌋)!(⌊8⌋+⌊8⌋+⌊8⌋)!(⌊9⌋+⌊9⌋+⌊9⌋)!=6=6=6=6=6=6=6=6=6=6或甚至更簡潔的操作
(0!+0!+0!)!((dxd1)!+(dxd1)!+(dxd1)!)!((dxd2)!+(dxd2)!+(dxd2)!)!((dxd3)!+(dxd3)!+(dxd3)!)!((dxd4)!+(dxd4)!+(dxd4)!)!((dxd5)!+(dxd5)!+(dxd5)!)!((dxd6)!+(dxd6)!+(dxd6)!)!((dxd7)!+(dxd7)!+(dxd7)!)!((dxd8)!+(dxd8)!+(dxd8)!)!((dxd9)!+(dxd9)!+(dxd9)!)!=6=6=6=6=6=6=6=6=6=6